题目内容
12.已知实数p>0,曲线C1:$\left\{\begin{array}{l}{x=2p{t}^{2}}\\{y=2pt}\end{array}\right.$(t为参数)上的点A(2,m),曲线C2:$\left\{\begin{array}{l}{x=\frac{p}{2}+6cosθ}\\{y=6sinθ}\end{array}\right.$(θ为参数)的圆心为点B,A、B两点间的距离等于圆C2的半径,则p=8.分析 由曲线C1:$\left\{\begin{array}{l}{x=2p{t}^{2}}\\{y=2pt}\end{array}\right.$(t为参数),可得y2=2px,把点A(2,m)代入可得:m2=4p,曲线C2:$\left\{\begin{array}{l}{x=\frac{p}{2}+6cosθ}\\{y=6sinθ}\end{array}\right.$(θ为参数),化为$(x-\frac{p}{2})^{2}+{y}^{2}$=36,可得圆心点B,半径r.利用两点之间的距离公式可得|AB|,利用A、B两点间的距离等于圆C2的半径,即可解出.
解答 解:由曲线C1:$\left\{\begin{array}{l}{x=2p{t}^{2}}\\{y=2pt}\end{array}\right.$(t为参数),可得y2=2px,把点A(2,m)代入可得:m2=4p,
曲线C2:$\left\{\begin{array}{l}{x=\frac{p}{2}+6cosθ}\\{y=6sinθ}\end{array}\right.$(θ为参数),化为$(x-\frac{p}{2})^{2}+{y}^{2}$=36,圆心点B$(\frac{p}{2},0)$,半径r=6.
|AB|=$\sqrt{(2-\frac{p}{2})^{2}+{m}^{2}}$=$\sqrt{(2-\frac{p}{2})^{2}+4p}$=$\sqrt{4+2p+\frac{{p}^{2}}{4}}$,
∵A、B两点间的距离等于圆C2的半径,
∴$\sqrt{4+2p+\frac{{p}^{2}}{4}}$=6,
解得p=8.
故答案为:8.
点评 本题考查了参数方程化为普通方程、两点之间的距离公式、圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P、Q,若∠PAQ=60°且$\overrightarrow{OQ}$=3$\overrightarrow{OP}$,则双曲线C的离心率为( )
如图,已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P、Q,若∠PAQ=60°且$\overrightarrow{OQ}$=3$\overrightarrow{OP}$,则双曲线C的离心率为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{\sqrt{39}}{6}$ | D. | $\sqrt{3}$ |
 如图,在地面上共线的三点A,B,C处测得一建筑物的仰角分别为30°,45°,60°,且AB=BC=60m,则建筑物的高度为( )
如图,在地面上共线的三点A,B,C处测得一建筑物的仰角分别为30°,45°,60°,且AB=BC=60m,则建筑物的高度为( )| A. | 15$\sqrt{6}$m | B. | 20$\sqrt{6}$m | C. | 25$\sqrt{6}$m | D. | 30$\sqrt{6}$m |
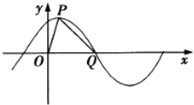 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,P是图象的最高点,Q为图象与x轴的交点,O为坐标原点,若OQ=4,OP=$\sqrt{5}$,PQ=$\sqrt{13}$.
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,P是图象的最高点,Q为图象与x轴的交点,O为坐标原点,若OQ=4,OP=$\sqrt{5}$,PQ=$\sqrt{13}$.