题目内容
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=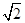 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
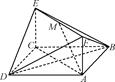
求证:(1)AM∥平面BDE;
(2)AM⊥平面BDF.
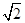 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
求证:(1)AM∥平面BDE;
(2)AM⊥平面BDF.
(1)见解析(2)见解析
(1)建立如图所示的空间直角坐标系,设AC∩BD=N,连结NE.
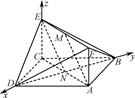
则N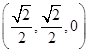 ,E(0,0,1),A(
,E(0,0,1),A(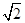 ,
,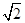 ,0),M
,0),M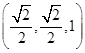 .
.
∴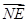 =
=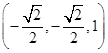 ,
,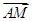 =
=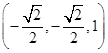 .
.
∴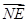 =
=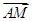 且NE与AM不共线.∴NE∥AM.
且NE与AM不共线.∴NE∥AM.
∵NE?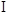 平面BDE,AM
平面BDE,AM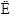 平面BDE,∴AM∥平面BDE.
平面BDE,∴AM∥平面BDE.
(2)由(1)知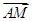 =
=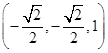 ,
,
∵D(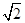 ,0,0),F(
,0,0),F(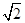 ,
,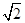 ,1),∴
,1),∴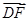 =(0,
=(0,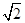 ,1),
,1),
∴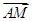 ·
·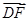 =0,∴AM⊥DF.同理AM⊥BF.又DF∩BF=F,∴AM⊥平面BDF.
=0,∴AM⊥DF.同理AM⊥BF.又DF∩BF=F,∴AM⊥平面BDF.

则N
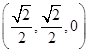 ,E(0,0,1),A(
,E(0,0,1),A(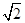 ,
,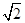 ,0),M
,0),M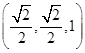 .
.∴
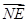 =
=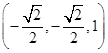 ,
,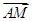 =
=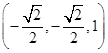 .
.∴
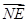 =
=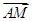 且NE与AM不共线.∴NE∥AM.
且NE与AM不共线.∴NE∥AM.∵NE?
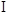 平面BDE,AM
平面BDE,AM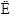 平面BDE,∴AM∥平面BDE.
平面BDE,∴AM∥平面BDE.(2)由(1)知
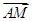 =
=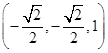 ,
,∵D(
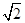 ,0,0),F(
,0,0),F(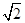 ,
,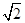 ,1),∴
,1),∴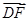 =(0,
=(0,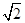 ,1),
,1),∴
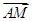 ·
·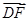 =0,∴AM⊥DF.同理AM⊥BF.又DF∩BF=F,∴AM⊥平面BDF.
=0,∴AM⊥DF.同理AM⊥BF.又DF∩BF=F,∴AM⊥平面BDF.
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
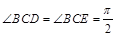 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.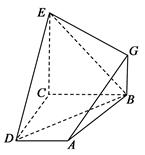
 平面BDE;
平面BDE; DE
DE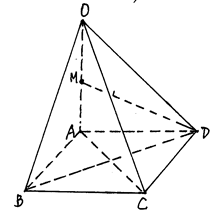
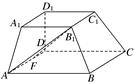
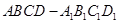 中
中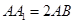 ,则
,则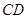 与平面
与平面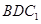 所成角的正弦值等于( )
所成角的正弦值等于( )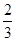
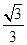
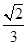
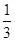
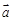 =(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )
=(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )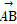 与
与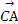 的夹角θ的大小是( )
的夹角θ的大小是( )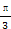
 π
π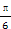
 π
π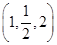 ,则m=________.
,则m=________.