题目内容
9.若不等式组$\left\{\begin{array}{l}x≥0\\ x+3y≥4\\ 3x+y≤4\end{array}$所表示的平面区域被直线y=kx+$\frac{4}{3}$分为面积比为1:2的两部分,则k的一个值为( )| A. | $\frac{7}{3}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | $\frac{3}{7}$ |
分析 作出不等式组对应的平面区域,求出阴影部分的面积,根据面积比是1:2,即可确定k的值.
解答 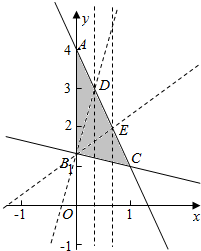 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
则A(0,4),B(0,$\frac{4}{3}$),
由$\left\{\begin{array}{l}{x+3y=4}\\{3x+y=4}\end{array}\right.$,解得C(1,1),
则三角形ABC的面积S=$\frac{1}{2}$×(4-$\frac{4}{3}$)×1=$\frac{4}{3}$,
∵平面区域被直线y=kx+$\frac{4}{3}$分成面积比是1:2的两部分,
∴面积较小的面积为$\frac{4}{3}×\frac{1}{3}=\frac{4}{9}$,
∵直线y=kx+$\frac{4}{3}$过定点B(0,$\frac{4}{3}$),
若△ABD的面积为$\frac{4}{9}$,则S=$\frac{1}{2}×\frac{8}{3}{x}_{D}=\frac{4}{9}$,解得xD=$\frac{1}{3}$,由$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{3x+y=4}\end{array}\right.$,
解得D($\frac{1}{3}$,3),此时BD的斜率k=$\frac{3-\frac{4}{3}}{\frac{1}{3}-0}=5$.
若△ABE的面积为$\frac{4}{3}×\frac{2}{3}=\frac{8}{9}$,则S=$\frac{1}{2}×\frac{8}{3}×{x}_{E}=\frac{8}{9}$,xE=$\frac{2}{3}$,
由$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{3x+y=4}\end{array}\right.$,
解得E($\frac{2}{3}$,2),此时BE的斜率k=1;
故k=5或k=1;
故选:C.
点评 本题主要考查线性规划的应用,根据三角形的面积公式求出满足条件的直线的位置关系是解决本题的关键.

| A. | a≤b≤c | B. | c≤b≤a | C. | b≤c≤a | D. | a≤c≤b |
| A. | (3,5) | B. | ($\frac{1}{2}$,+∞) | C. | (-1,2) | D. | ($\frac{1}{3}$,1) |