题目内容
8．已知实数x、y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$则目标函数$z=\frac{y+2}{x-5}$的最大值为（ ）| A． | 3 | B． | 4 | C． | -3 | D． | $-\frac{1}{2}$ |
分析 通过作出约束条件的图象△ABC，利用目标函数$z=\frac{y+2}{x-5}$即为过点Q（5，-2）且与△ABC相交的直线的斜率，计算即得结论．
解答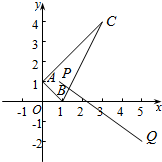 
解：依题意，作出约束条件的图象，
其中A（0，1），B（1，0），C（3，4），
目标函数$z=\frac{y+2}{x-5}$即为过点Q（5，-2）且与△ABC相交的直线的斜率，
显然过B、Q两点的直线的斜率z最大，最大值为$\frac{0+2}{1-5}$=-$\frac{1}{2}$，
故选：D．
点评 本题考查简单线性规划，考查数形结合能力，弄清目标函数的意义是解决本题的关键，注意解题方法的积累，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
3．已知圆锥高为h，底面圆半径、锥高、母线长构成等比数列，则圆锥的侧面积是（ ）
| A． | $\frac{1}{3}π{h^2}$ | B． | $\frac{1}{2}π{h^2}$ | C． | πh2 | D． | 2πh2 |