题目内容
13.已知平面向量$\overrightarrow{α}$,$\overrightarrow{β}$($\overrightarrow{α}$≠$\overrightarrow{β}$)满足|$\overrightarrow{α}$|=$\sqrt{3}$且$\overrightarrow{α}$与$\overrightarrow{β}$-$\overrightarrow{α}$的夹角为150°,则|m$\overrightarrow{α}$+(1-m)$\overrightarrow{β}$|的取值范围是$[\frac{{\sqrt{3}}}{2},+∞)$.分析 如图所示,不妨设$\overrightarrow{α}$=($\sqrt{3}$,0),$\overrightarrow{OB}$=$\overrightarrow{β}$.$\overrightarrow{α}$与$\overrightarrow{β}$-$\overrightarrow{α}$的夹角为150°,可得∠OAB=30°.由于$\overrightarrow{OC}$=$m\overrightarrow{α}$+(1-m)$\overrightarrow{β}$.可知:点C在直线AB上,当且仅当OC⊥AB时,$|\overrightarrow{OC}|$取得最小值,即可得出.
解答 解:如图所示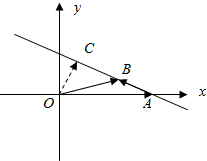
不妨设$\overrightarrow{α}$=($\sqrt{3}$,0),$\overrightarrow{OB}$=$\overrightarrow{β}$.
$\overrightarrow{OC}$=$m\overrightarrow{α}$+(1-m)$\overrightarrow{β}$.
∵$\overrightarrow{α}$与$\overrightarrow{β}$-$\overrightarrow{α}$的夹角为150°,
∴∠OAB=30°.
由于$\overrightarrow{OC}$=$m\overrightarrow{α}$+(1-m)$\overrightarrow{β}$.
可知:点C在直线AB上,
当且仅当OC⊥AB时,$|\overrightarrow{OC}|$取得最小值,此时$|\overrightarrow{OC}|$=$|\overrightarrow{OA}|sin3{0}^{°}$=$\frac{\sqrt{3}}{2}$.
∴|m$\overrightarrow{α}$+(1-m)$\overrightarrow{β}$|的取值范围是$[\frac{{\sqrt{3}}}{2},+∞)$.
故答案为:$[\frac{{\sqrt{3}}}{2},+∞)$.
点评 本题考查了向量的夹角、直角三角形的边角关系、向量共线定理,考查了推理能力与计算能力,属于中档题.

 金钥匙试卷系列答案
金钥匙试卷系列答案| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 线段 |
| A. | 3 | B. | 4 | C. | -3 | D. | $-\frac{1}{2}$ |
| A. | [0,2] | B. | [-1,1] | C. | [-2,2] | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
| A. | y=x3 | B. | y=-x2 | C. | y=2x | D. | y=ln|x| |
