题目内容
16．下列函数中，既是偶函数，又是在区间（0，+∞）上单调递减的函数是（ ）| A． | y=|x| | B． | y=-x3 | C． | y=-（x+1）2 | D． | y=-x2 |
分析 根据函数奇偶性和单调性的性质进行判断即可．
解答 解：A．y=|x|是偶函数，在区间（0，+∞）上单调递增，不满足条件．
B．y=-x3是奇函数，不满足条件．
C．y=-（x+1）2是非奇非偶函数，不满足条件．
D．y=-x2是偶函数，在区间（0，+∞）上单调递减，满足条件．
故选：D
点评 本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数的奇偶性和单调性．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
6．
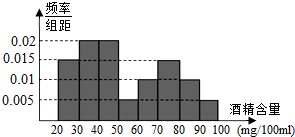据《南通日报》报道，2015年1月1日至1月31日，市交管部门共抽查了1000辆车，查出酒后驾车和醉酒驾车的驾驶员80人，如图是对这80人血液中酒精含量进行检查所得结果的频率分布直方图．（酒精含量≥80mg/100ml为醉酒驾车）
（1）根据频率分布直方图完成下表：
（2）根据上述数据，求此次抽查的1000人中属于醉酒驾车的概率；
（3）若用分层抽样的方法从血液酒精浓度在[70，90）范围内的驾驶员中抽取一个容量为5的样本，并将该样本看成一个总体，从中任取2人，求恰有1人属于醉酒驾车的概率．
据《南通日报》报道，2015年1月1日至1月31日，市交管部门共抽查了1000辆车，查出酒后驾车和醉酒驾车的驾驶员80人，如图是对这80人血液中酒精含量进行检查所得结果的频率分布直方图．（酒精含量≥80mg/100ml为醉酒驾车）（1）根据频率分布直方图完成下表：
| 酒精含量（单位：mg/100ml） | [20，30） | [30，40） | [40，50） | [50，60） |
| 人数 | 16 | 16 | 4 | |
| 酒精含量（单位：mg/100ml） | [60，70） | [70，80） | [80，90） | [90，100] |
| 人数 | 4 |
（3）若用分层抽样的方法从血液酒精浓度在[70，90）范围内的驾驶员中抽取一个容量为5的样本，并将该样本看成一个总体，从中任取2人，求恰有1人属于醉酒驾车的概率．
7．设S=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$+$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$+…+$\sqrt{1+\frac{1}{201{4}^{2}}+\frac{1}{201{5}^{2}}}$，则不大于S的最大整数等于（ ）
| A． | 2016 | B． | 2015 | C． | 2014 | D． | 2013 |
8．已知数列{an}的通项公式为an=n+$\frac{c}{n}$，若对任意n∈N+，都有an≥a3，则实数c的取值范围是（ ）
| A． | [6，12] | B． | （6，12） | C． | [5，12] | D． | （5，12） |
5．已知a＜b＜0，则下列不等式一定成立的是（ ）
| A． | a2＜ab | B． | |a|＜|b| | C． | $\frac{1}{a}＞\frac{1}{b}$ | D． | ${（{\frac{1}{2}}）^a}＜{（{\frac{1}{2}}）^b}$ |