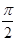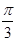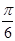题目内容
△ABC中,下列说法正确的是( )
| A.asinA=bsinB |
| B.若A>B,则sinA>sinB |
| C.若A>B,则cosA>cosB |
| D.若sinB+sinC=sin2A,则b+c=a2 |
对于A,asinA=bsinB,由正弦定理可知,a2=b2,即a=b,显然三角形是等腰三角形,故A不正确;
对于B:△ABC中,若A>B,分两种情况:
当0<B<A≤90°,正弦函数sinx为单调递增区间,显然sinA>sinB;
当0<B<90°<A,设B=90°-x,A=90°+y(x与y均为大于0,小于90°的角),
sinB=sin(90°-x)=cosx,sinA=sin(90°+y)=cosy,
∵0<A+B<180°,则0<90°-x+90°+y<180,∴x>y,
由余弦函数cosx在(0,90°)为单调递减函数,
∴cosx<cosy,即sinB<sinA,
所以B正确;
对于C,不妨令A=120°,B=30°,满足A>B,但是cos120°=-
<cos30°=
,所以C不正确;
对于D,sinB+sinC=sin2A,由正弦定理可知,(b+c)2R=a2,当R=
时,有b+c=a2,所以D不正确;
综上,正确结果为B.
故选B.
对于B:△ABC中,若A>B,分两种情况:
当0<B<A≤90°,正弦函数sinx为单调递增区间,显然sinA>sinB;
当0<B<90°<A,设B=90°-x,A=90°+y(x与y均为大于0,小于90°的角),
sinB=sin(90°-x)=cosx,sinA=sin(90°+y)=cosy,
∵0<A+B<180°,则0<90°-x+90°+y<180,∴x>y,
由余弦函数cosx在(0,90°)为单调递减函数,
∴cosx<cosy,即sinB<sinA,
所以B正确;
对于C,不妨令A=120°,B=30°,满足A>B,但是cos120°=-
| 1 |
| 2 |
| ||
| 2 |
对于D,sinB+sinC=sin2A,由正弦定理可知,(b+c)2R=a2,当R=
| 1 |
| 2 |
综上,正确结果为B.
故选B.

练习册系列答案
相关题目
 AB
AB C中,若0
C中,若0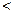 tanAtanB
tanAtanB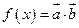 ,其中
,其中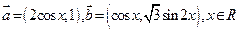 (1) 求
(1) 求 的最大值;(2)在
的最大值;(2)在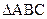 中,
中,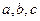 分别是角
分别是角 的对边,且f(A)=2,a=,b+c=3,求b,c的值
的对边,且f(A)=2,a=,b+c=3,求b,c的值 ,c=2,A=60°,求a,b的值;(2)若acosA=bcosB,试判断△ABC的形状,证明你的结论.
,c=2,A=60°,求a,b的值;(2)若acosA=bcosB,试判断△ABC的形状,证明你的结论.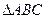 的三内角
的三内角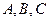 的对边边长分别为
的对边边长分别为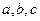 ,若
,若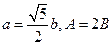 ,则
,则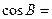 ( )
( )
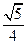
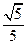

 的内角A,B,C所对的边分别为a,b,c,若
的内角A,B,C所对的边分别为a,b,c,若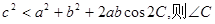 的可能取值为( ).
的可能取值为( ).