题目内容
根据下列条件,判断三角形解的情况,其中正确的是( )
| A.a=8,b=16,A=30°有两解 |
| B.a=18,b=20,A=60°有一解 |
| C.a=30,b=25,A=150°有一解 |
| D.a=5,b=2,A=90°无解 |
若a=8,b=16,A=30°,由正弦定理可得
=
,
解得sinB=1,∴B=
,故三角形有唯一解,故A不正确.
若a=18,b=20,A=60°,由正弦定理可得
=
,解得sinB=
.
再由大边对大角可得B>A,故B可以是锐角,也可以是钝角,故三角形有2解,故B不正确.
若a=30,b=25,A=150°,由正弦定理可得
=
,解得sinB=
.
再由B为锐角,可得三角形有唯一解,故C正确.
若 a=5,b=2,A=90°,则由正弦定理可得
=
,求得sinB=
,
再由大边对大角可得B为锐角,故三角形有唯一解,故D不正确,
故选 C.
| 8 |
| sin30° |
| 16 |
| sinB |
解得sinB=1,∴B=
| π |
| 2 |
若a=18,b=20,A=60°,由正弦定理可得
| 18 |
| sin60° |
| 20 |
| sinB |
5
| ||
| 9 |
再由大边对大角可得B>A,故B可以是锐角,也可以是钝角,故三角形有2解,故B不正确.
若a=30,b=25,A=150°,由正弦定理可得
| 30 |
| sin150° |
| 25 |
| sinB |
| 5 |
| 12 |
再由B为锐角,可得三角形有唯一解,故C正确.
若 a=5,b=2,A=90°,则由正弦定理可得
| 5 |
| sin90° |
| 2 |
| sinB |
| 2 |
| 5 |
再由大边对大角可得B为锐角,故三角形有唯一解,故D不正确,
故选 C.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
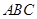 中,内角
中,内角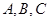 的对边分别为
的对边分别为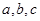 ,已知
,已知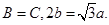
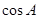 的值;(2)
的值;(2)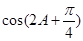 的值.
的值. 中,角
中,角 所对的边分别为
所对的边分别为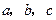 ,已知
,已知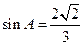 ,(1)求
,(1)求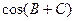 的值;(2)若
的值;(2)若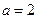 ,
,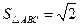 ,求
,求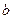 的值.
的值.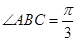 ,
,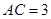 ,
,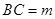 的
的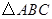 恰有一解,则实数
恰有一解,则实数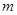 的取值范围是 .
的取值范围是 .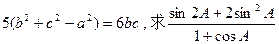 的值。
的值。 中,
中, ,则
,则 等于__________.
等于__________.