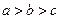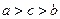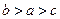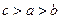题目内容
已知f(x)是偶函数,x ÎR,若将f(x)的图象向右平移一个单位又得到一个奇函
数,又f(2)=-1,则f(1)+ f(2)+ f(3)+…+ f(2011)= ( )
数,又f(2)=-1,则f(1)+ f(2)+ f(3)+…+ f(2011)= ( )
| A.-1003 | B.1003 | C.1 | D.-1 |
D
解:∵将f(x)的图象向右平移一个单位得到一个奇函数,
即f(x-1)是奇函数,∴f(-x-1)=-f(x-1),
又f(x)是偶函数,∴f(-x-1)=f(x+1),
∴f(x+1))=-f(x-1),
∴f((x-1)+4)=-f((x-1)+2)=f(x-1),可得f(x+4)=f(x),
∴函数f(x)的周期为4,
∵平移前f(x)是偶函数,f(x-1)是奇函数,x∈R,∴f(-1)=f(1)=f(3)=0,
f(0)=-f(-2)=-f(2)=1,
∴f(1)+f(2)+f(3)+…+f(2006)=501(f(1)+f(2)+f(3)+f(4))+f(1)+f(2)=-1,
故选D.

练习册系列答案
相关题目
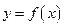 是定义在
是定义在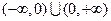 上的奇函数,当
上的奇函数,当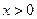 时,
时,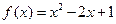 。
。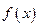 的解析式;
的解析式;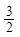 ,0)时,f(x)=log2(-3x+1),则f(2011)=( )
,0)时,f(x)=log2(-3x+1),则f(2011)=( )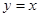
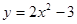
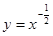
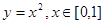
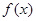 是
是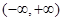 上的偶函数,若对于
上的偶函数,若对于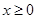 ,都有
,都有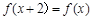 ,且当
,且当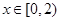 时,
时,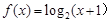 ,则
,则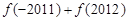 的值为
的值为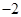
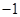
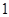
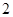
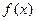 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且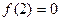 在区间(0,6)内整数
在区间(0,6)内整数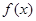 定义域为R,则
定义域为R,则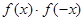 一定为 (
一定为 ( 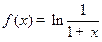 ,那么当xÎ(-1,0)时,f(x)=
,那么当xÎ(-1,0)时,f(x)= 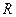 的函数
的函数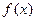 为偶函数,且当
为偶函数,且当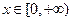 时,
时,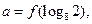
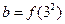 ,
,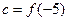 ,则
,则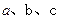 的大小关系是( )
的大小关系是( )