题目内容
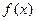 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且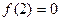 在区间(0,6)内整数
在区间(0,6)内整数解的个数是 ( )
| A.2 | B.3 | C.4 | D.5 |
D
∵f(x)是奇函数,∴f(0)=0
∵f(x)是以3为周期,f(2)=0
∴f(3)=f(0+3)=f(0)=0 f(5)=f(2+3)=f(2)=0
∵f(-1)=f(2-3)=f(2)=0;f(x)是奇函数,f(-1)=-f(1)=0。∴f(1)=0
f(4)=f(1+3)=f(1)=0
∵f(x)是以3为周期,∴f(1.5)=f(1.5-3)=f(-1.5)=-f(1.5)
也就是f(1.5)=-f(1.5),即2f(1.5)=0, f(1.5)=0 f(4.5)=f(1.5+3)=0
由此可见,f(x)=0在区间(0,6)内的解有7个,分别是:1、2、3、4、5、1.5、4.5
整数解有5个
∵f(x)是以3为周期,f(2)=0
∴f(3)=f(0+3)=f(0)=0 f(5)=f(2+3)=f(2)=0
∵f(-1)=f(2-3)=f(2)=0;f(x)是奇函数,f(-1)=-f(1)=0。∴f(1)=0
f(4)=f(1+3)=f(1)=0
∵f(x)是以3为周期,∴f(1.5)=f(1.5-3)=f(-1.5)=-f(1.5)
也就是f(1.5)=-f(1.5),即2f(1.5)=0, f(1.5)=0 f(4.5)=f(1.5+3)=0
由此可见,f(x)=0在区间(0,6)内的解有7个,分别是:1、2、3、4、5、1.5、4.5
整数解有5个

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
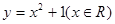
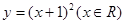

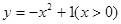
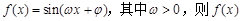 是偶函数的重要条件是( )
是偶函数的重要条件是( )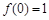
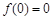
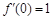
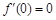
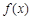 的图像关于点
的图像关于点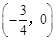 对称,且满足
对称,且满足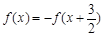 ,
,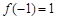 ,
,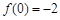 ,则
,则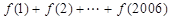 的值为
的值为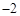

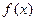 是定义在
是定义在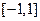 上的奇函数,且
上的奇函数,且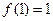 ,若
,若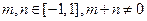 时,有
时,有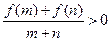
 .
.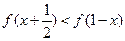 ;
;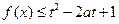 对所有
对所有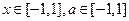 恒成立,求实数
恒成立,求实数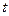 的取值范围.
的取值范围.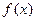 是周期为2的奇函数,当0≤
是周期为2的奇函数,当0≤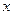 ≤1时,
≤1时,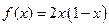 ,则
,则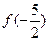 =
=



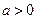 ,且
,且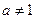 ,
,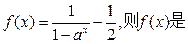
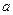 有关
有关