题目内容
已知椭圆 的离心率为
的离心率为 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设 ,过点
,过点 作与
作与 轴不重合的直线
轴不重合的直线 交椭圆于
交椭圆于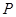 、
、 两点,连结
两点,连结 、
、 分别交直线
分别交直线 于
于 、
、 两点.试问直线
两点.试问直线 、
、 的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由.
的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由.
(1) ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)由直线和圆相切,求 ,再由离心率
,再由离心率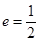 ,得
,得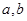 ,从而求
,从而求 ,进而求椭圆
,进而求椭圆 的方程;(2)要说明直线
的方程;(2)要说明直线 、
、 的斜率之积是否为定值,关键是确定
的斜率之积是否为定值,关键是确定 、
、 两点的坐标.首先设直线
两点的坐标.首先设直线 的方程,并与椭圆联立,设
的方程,并与椭圆联立,设 ,利用三点共线确定
,利用三点共线确定 、
、 两点的坐标的坐标,再计算直线
两点的坐标的坐标,再计算直线 、
、 的斜率之积,这时会涉及到
的斜率之积,这时会涉及到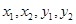 ,结合根与系数的关系,研究其值是否为定值即可.
,结合根与系数的关系,研究其值是否为定值即可.
试题解析:(1)
 ,故
,故 4分
4分
(2)设 ,若直线
,若直线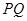 与纵轴垂直,
与纵轴垂直, 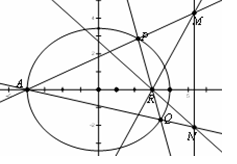
则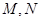 中有一点与
中有一点与 重合,与题意不符,
重合,与题意不符,
故可设直线 . 5分
. 5分
将其与椭圆方程联立,消去 得:
得: 6分
6分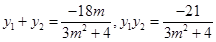 7分
7分
由 三点共线可知,
三点共线可知, ,
,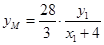 , 8分
, 8分
同理可得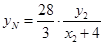 9分
9分 10分
10分
而 11分
11分
所以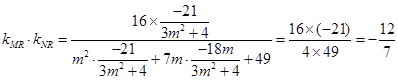
故直线 、
、 的斜率为定值
的斜率为定值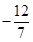 . 13分
. 13分
考点:1、椭圆的标准方程和简单几何性质;2、直线和椭圆的位置关系.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
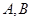 是抛物线
是抛物线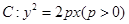 上不同的两点,点
上不同的两点,点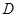 在抛物线
在抛物线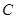 的准线
的准线 上,且焦点
上,且焦点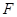 到直线
到直线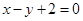 的距离为
的距离为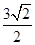 .
.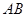 过焦点
过焦点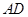 过原点
过原点 ;③直线
;③直线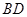 平行
平行 轴.
轴.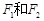 ,且点
,且点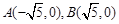 在椭圆C上,又
在椭圆C上,又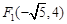 .
.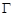 的方程;
的方程;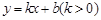 与曲线
与曲线 :
: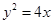 和
和 :
:
 的焦点分别为
的焦点分别为 ,
, 交于
交于 两点(
两点( 为坐标原点),且
为坐标原点),且
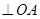 .
. ,交
,交 ,点
,点 坐标为
坐标为 ,求△
,求△ 面积的最小值.
面积的最小值. = 2
= 2 ,求直线l的方程.
,求直线l的方程.
 的右焦点
的右焦点
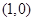 ,长轴的左、右端点分别为
,长轴的左、右端点分别为 ,且
,且 .
. 的方程;
的方程; (
( )的直线
)的直线 交椭圆
交椭圆 两点,弦
两点,弦 的垂直平分线与
的垂直平分线与 轴相交于
轴相交于 点. 试问椭圆
点. 试问椭圆 使得四边形
使得四边形 为菱形?若存在,求
为菱形?若存在,求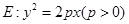 的准线与x轴交于点M,过点M作圆
的准线与x轴交于点M,过点M作圆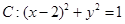 的两条切线,切点为A、B,
的两条切线,切点为A、B,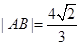 .
.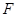
 与分别在
与分别在 轴、
轴、 轴上的动点
轴上的动点 满足:
满足: ,动点
,动点 满足
满足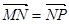 .
.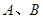 两点,直线
两点,直线 与直线
与直线 分别交于点
分别交于点 (
( 为坐标原点);
为坐标原点); 为直径的圆的位置关系;
为直径的圆的位置关系; 是否为定值?并证明你的结论.
是否为定值?并证明你的结论. 经过点
经过点 ,其左、右顶点分别是
,其左、右顶点分别是 、
、 ,左、右焦点分别是
,左、右焦点分别是 、
、 ,
, (异于
(异于 交直线
交直线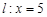 于
于 、
、 两点,若
两点,若 成等比数列.
成等比数列.
 为直径的圆过点
为直径的圆过点