题目内容
已知点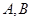 是抛物线
是抛物线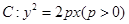 上不同的两点,点
上不同的两点,点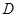 在抛物线
在抛物线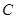 的准线
的准线 上,且焦点
上,且焦点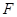 到直线
到直线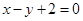 的距离为
的距离为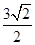 .
.
(I)求抛物线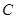 的方程;
的方程;
(2)现给出以下三个论断:①直线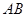 过焦点
过焦点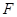 ;②直线
;②直线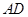 过原点
过原点 ;③直线
;③直线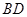 平行
平行 轴.
轴.
请你以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题,并加以证明.
(1)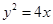 ;(2)参考解析
;(2)参考解析
解析试题分析:(1)由点F到直线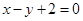 的距离为
的距离为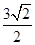 可求得抛物线中
可求得抛物线中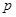 .从而得到抛物线方程.
.从而得到抛物线方程.
(2)根据题意共有三种情况:i) ①直线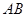 过焦点
过焦点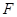 ;②直线
;②直线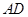 过原点
过原点 .由直线AB与抛物线的方程联立结合韦达定理,表示出点D,B的坐标即可得到③直线
.由直线AB与抛物线的方程联立结合韦达定理,表示出点D,B的坐标即可得到③直线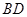 平行
平行 轴.ii) ①直线
轴.ii) ①直线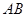 过焦点
过焦点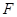 ;③直线
;③直线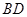 平行
平行 轴同样是表达出点D,B的坐标即可得到点A,O,D三点共线,即可得到结论.iii) ②直线
轴同样是表达出点D,B的坐标即可得到点A,O,D三点共线,即可得到结论.iii) ②直线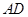 过原点
过原点 ;③直线
;③直线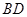 平行
平行 轴表达出点A,B的坐标关系即可得到点A,F,B三点共线,即得到结论.
轴表达出点A,B的坐标关系即可得到点A,F,B三点共线,即得到结论.
(I)因为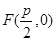 , 依题意得
, 依题意得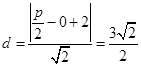 , 2分
, 2分
解得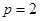 ,所以抛物线
,所以抛物线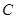 的方程为
的方程为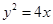 4分
4分
(2)①命题:若直线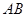 过焦点
过焦点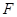 ,且直线
,且直线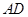 过原点
过原点 ,则直线
,则直线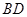 平行
平行 轴.
轴.
5分
设直线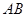 的方程为
的方程为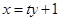 ,
,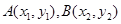 , 6分
, 6分
由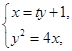 得
得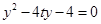 ,
,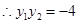 , 8分
, 8分
直线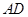 的方程为
的方程为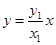 , 9分
, 9分
所以点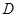 的坐标为
的坐标为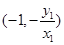 ,
,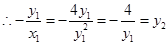 , 12分
, 12分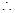 直线
直线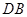 平行于
平行于 轴. 13分
轴. 13分
②命题:若直线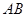 过焦点
过焦点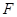 ,且直线
,且直线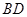 平行
平行 轴,则直线
轴,则直线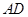 过原点
过原点 .
.
5分
设直线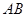 的方程为
的方程为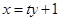 ,
,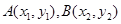 , 6分
, 6分
由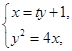 得
得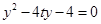 ,
,
练习册系列答案
相关题目
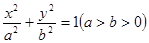 的右焦点为
的右焦点为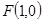 ,离心率
,离心率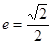 ,
,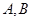 是椭圆上的动点.
是椭圆上的动点.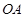 与
与 的斜率乘积
的斜率乘积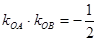 ,动点
,动点 满足
满足 ,(其中实数
,(其中实数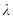 为常数).问是否存在两个定点
为常数).问是否存在两个定点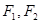 ,使得
,使得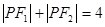 ?若存在,求
?若存在,求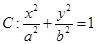
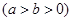 的离心率为
的离心率为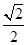 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线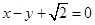 相切.
相切.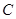 的方程;
的方程;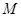 (2,0)的直线与椭圆
(2,0)的直线与椭圆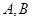 ,设
,设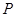 为椭圆上一点,且满足
为椭圆上一点,且满足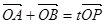 (
(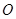 为坐标原点),当
为坐标原点),当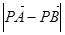 <
<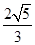 时,求实数
时,求实数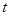 取值范围.
取值范围.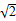 )上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
)上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.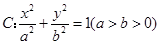 经过点P(1.
经过点P(1. ),离心率e=
),离心率e= ,直线l的方程为x=4.
,直线l的方程为x=4.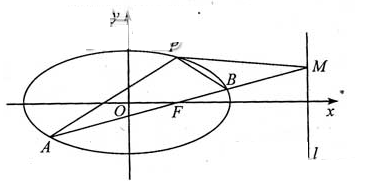
 .问:是否存在常数λ,使得
.问:是否存在常数λ,使得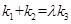 ?若存在,求λ的值;若不存在,说明理由.
?若存在,求λ的值;若不存在,说明理由. 的焦点在x轴上.
的焦点在x轴上.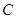 的中心在原点
的中心在原点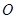 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为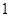 .
.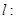
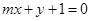 与椭圆
与椭圆 两点,是否存在实数
两点,是否存在实数 ,使
,使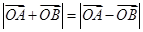 成立?若存在,求
成立?若存在,求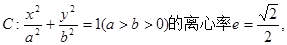 左、右焦点分别为F1、F2,点P(2,
左、右焦点分别为F1、F2,点P(2,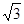 ),点F2在线段PF1的中垂线上.
),点F2在线段PF1的中垂线上. 与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标.
与椭圆C交于M、N两点,直线F2M与F2N的斜率互为相反数,求证:直线l过定点,并求该定点的坐标. 的离心率为
的离心率为 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线 相切.
相切. 的方程;
的方程; ,过点
,过点 作与
作与 轴不重合的直线
轴不重合的直线 交椭圆于
交椭圆于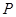 、
、 两点,连结
两点,连结 、
、 分别交直线
分别交直线 于
于 、
、 两点.试问直线
两点.试问直线 、
、 的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由.
的斜率之积是否为定值,若是,求出该定值;若不是,请说明理由.