题目内容
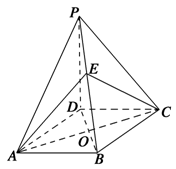
(本大题12分)如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求直线 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;
(2)求证:平面A B1D1∥平面EFG;
(3)求证:平面AA1C⊥面EFG .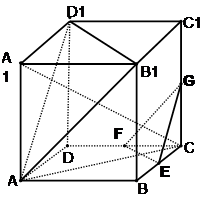
(1)求直线
 C与平面ABCD所成角的正弦的值;
C与平面ABCD所成角的正弦的值;(2)求证:平面A B1D1∥平面EFG;
(3)求证:平面AA1C⊥面EFG .
(1)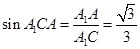 ; (2)见解析;(3)见解析。
; (2)见解析;(3)见解析。
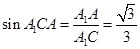 ; (2)见解析;(3)见解析。
; (2)见解析;(3)见解析。试题分析:(1)因为
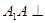 平面ABCD,所以
平面ABCD,所以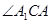 为
为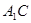 与平面ABCD所成角,
与平面ABCD所成角,然后解三角形求出此角即可.
(2)证明面面平行根据判定定理只须证明平面平面A B1D1内两条相交直线
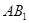 和
和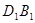 分别平行于平面EFG即可.在证明线面平行时又转化为证明线线平行.
分别平行于平面EFG即可.在证明线面平行时又转化为证明线线平行.(3)易证:BD
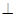 平面AA1C,再证明EF//BD,因而可证出平面AA1C⊥面EFG.
平面AA1C,再证明EF//BD,因而可证出平面AA1C⊥面EFG.(1)∵
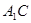
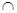 平面ABCD=C,在正方体ABCD-A1B1C1D1
平面ABCD=C,在正方体ABCD-A1B1C1D1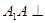 平面ABCD
平面ABCD∴AC为
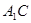 在平面ABCD的射影
在平面ABCD的射影∴
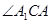 为
为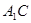 与平面ABCD所成角……….2分
与平面ABCD所成角……….2分正方体的棱长为

∴AC=
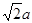 ,
,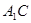 =
=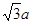
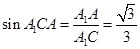 ………..4分
………..4分(2)在正方体ABCD-A1B1C1D1
连接BD,
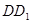 ∥
∥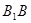 ,
,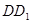 =
=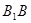
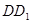
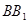 为平行四边形
为平行四边形∴
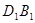 ∥
∥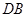 ∵E,F分别为BC,CD的中点
∵E,F分别为BC,CD的中点∴EF∥BD∴EF∥
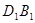 …………3分
…………3分∵EF
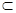 平面GEF,
平面GEF,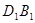
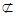 平面GEF
平面GEF∴
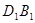 ∥平面GEF …………7分
∥平面GEF …………7分同理
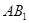 ∥平面GEF∵
∥平面GEF∵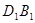
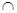
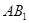 =
=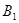
∴平面A B1D1∥平面EFG ……………9分
(3)在正方体ABCD-A1B1C1D1∴
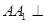 平面ABCD
平面ABCD∵EF
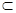 平面ABCD
平面ABCD∴
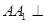 EF …………10分
EF …………10分∵ABCD为正方形
∴AC
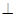 BD
BD∵EF∥BD
∴AC
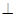 EF ………..11分
EF ………..11分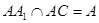
∴EF
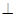 平面AA1C
平面AA1C∵EF
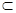 平面EFG
平面EFG∴平面AA1C⊥面EFG …………….12分.
点评:斜线与平面所成的角就是斜线与它在这个平面内的射影所成的角,因而关键是找到它在这个平面内的射影.面面垂直(平行)证明要转化为证明线面垂直(平行)再转化为线线垂直(平行).

练习册系列答案
相关题目
 ,中,
,中,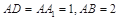 ,点
,点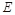 在棱AB上移动.
在棱AB上移动.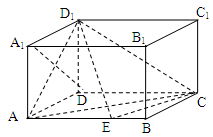
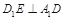 ;
; 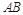 的中点时,求点
的中点时,求点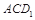 的距离;
的距离; 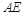 等于何值时,二面角
等于何值时,二面角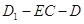 的大小为
的大小为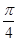 .
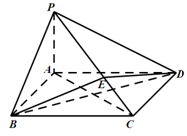
.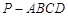 中,底面
中,底面 为矩形,
为矩形,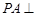 平面
平面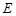 在线段
在线段 上,
上,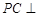 平面
平面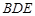 .
.
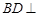 平面
平面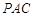 ;
;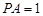 ,
,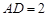 ,求二面角
,求二面角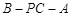 的正切值.
的正切值. ,使得平面
,使得平面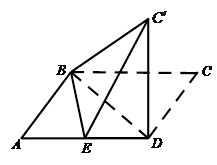
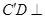 平面ABD;
平面ABD;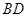 与平面
与平面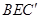 所成角的正弦值;
所成角的正弦值; 的余弦值.
的余弦值.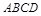 中,
中,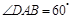 .点
.点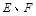 分别在边
分别在边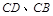 上,点
上,点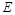 与点
与点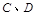 不重合,
不重合,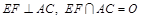 .沿
.沿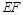 将
将 翻折到
翻折到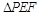 的位置,使平面
的位置,使平面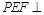 平面
平面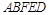 .
.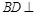 平面
平面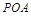 ;
;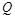 满足
满足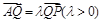 ,试探究:当
,试探究:当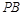 取得最小值时,直线
取得最小值时,直线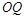 与平面
与平面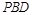 所成角的大小是否一定大于
所成角的大小是否一定大于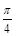 ?并说明理由.
?并说明理由.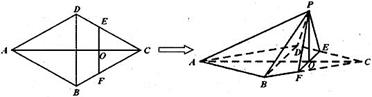
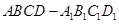 中,
中,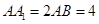 ,点
,点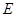 在
在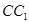 上且
上且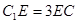 .
.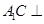 平面
平面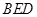 ;
;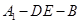 的余弦值大小.
的余弦值大小.
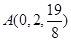 ,
,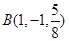 ,
,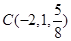 是平面
是平面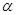 内的三点,设平面
内的三点,设平面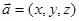 ,则
,则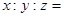 .
.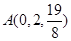 ,
,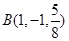 ,
,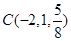 是平面
是平面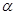 内的三点,设平面
内的三点,设平面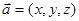 ,则
,则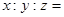 ______________
______________