题目内容
【题目】如图,四边形![]() 是直角梯形,
是直角梯形,![]() 平面
平面![]() ,
,![]()

(1)求直线![]() 与平面
与平面![]() 所成角的余弦;
所成角的余弦;
(2)求平面![]() 和平面
和平面![]() 所成角的余弦.
所成角的余弦.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)建立空间直角坐标系,由题意可得![]() 则
则![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,据此计算可得
,据此计算可得![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]()
(2)平面![]() 的一个法向量为
的一个法向量为![]() ,计算可得平面
,计算可得平面![]() 的一个法向量为
的一个法向量为![]() 据此计算可得平面
据此计算可得平面![]() 和平面
和平面![]() 所成角的余弦值为
所成角的余弦值为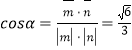 .
.
试题解析:
(1) 如图建系,
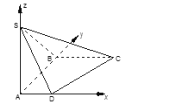
S(0,0,2), C(2,2,0), D(1,0,0),![]()
![]() 平面
平面![]() ,故平面
,故平面![]() 的一个法向量为
的一个法向量为![]()
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,由题意可得:
,由题意可得: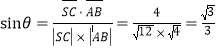 ,
,
故![]() ,即
,即![]() 与平面
与平面![]() 所成的角余弦为
所成的角余弦为![]() .
.
(2)平面![]() 的一个法向量为
的一个法向量为![]()
![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由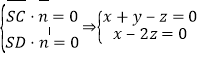 令
令![]() 可得平面
可得平面![]() 的一个法向量为
的一个法向量为
![]()
显然,平面![]() 和平面
和平面![]() 所成角为锐角,不妨设为
所成角为锐角,不妨设为![]() 则
则
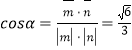
即平面![]() 和平面
和平面![]() 所成角的余弦
所成角的余弦![]() .
.

练习册系列答案
相关题目
【题目】某校乒乓球队有3名男同学A,B,C和3名女同学X,Y,Z,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加乒乓球比赛(每人被选到的可能性相同).
(1)用表中字母列举出所有可能的结果;
(2)设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.


