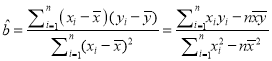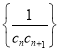��Ŀ����
����Ŀ��1979�꣬��������ʿ���й��Ƽ���ѧ��������һ����Ȥ�⣺5ֻ���ӷ�һ�����ӣ���ôҲ���ֳܷ�5�ȷݣ�ֻ����ȥ˯�������ڶ����ٷ֣�ҹ��1ֻ����͵͵���������ȳԵ�һ�����ӣ�Ȼ����ֳ�5�ȷݣ������Լ���һ�ݾ�ȥ˯���ˣ���2ֻ����������������ʣ������ӳԵ�һ����Ҳ�����ӷֳ�5�ȷݣ������Լ���һ��˯��ȥ�ˣ��Ժ��3ֻ���Ӷ��Ⱥ��մ˰������ʣ���������ж��ٸ����ӣ��������ʣ�¶��ٸ����ӣ�
���𰸡��������������![]() �����Ӷ��������ʣ��
�����Ӷ��������ʣ��![]() ��.
��.
�����������������
��ԭ����ת��Ϊ���еĵ��ƹ�ϵ����Ŀ��Ȼ���ϵ��ƹ�ϵʽ���ۿɵ��������������![]() �����Ӷ��������ʣ��
�����Ӷ��������ʣ��![]() ��.
��.
���������
���������������![]() �����ӣ�����ÿ�η�ʣ�µ���������Ϊ
�����ӣ�����ÿ�η�ʣ�µ���������Ϊ![]() ���õ�һ������
���õ�һ������![]() �������⣬��֪���еĵ��ƹ�ʽ��
�������⣬��֪���еĵ��ƹ�ʽ�� ![]() ����
����![]() ��
��
����������![]() .
.
��![]() ����
����![]() Ϊ���ȵĵȱ����У�����
Ϊ���ȵĵȱ����У�����![]() ��
��
��ʹ![]() ��Ӧ��
��Ӧ��![]() ��
��
���������������![]() �����Ӷ��������ʣ��
�����Ӷ��������ʣ��![]() ��.
��.

����Ŀ��ij��Ʒ�Ĺ�����x�����۶�y��ͳ�����������
������x����Ԫ�� | 4 | 2 | 3 | 5 |
���۶�y����Ԫ�� | 49 | 26 | 39 | 54 |
�����ϱ��ɵûع鷽�� ![]() =
= ![]() x+
x+ ![]() �е�
�е� ![]() Ϊ9.4���ݴ�ģ��Ԥ��������Ϊ6��Ԫʱ���۶�Ϊ�� ��
Ϊ9.4���ݴ�ģ��Ԥ��������Ϊ6��Ԫʱ���۶�Ϊ�� ��
A.63.6��Ԫ
B.67.7��Ԫ
C.65.5��Ԫ
D.72.0��Ԫ