Question

【题目】已知且，直线: ，圆: ．

（Ⅰ）若，请判断直线与圆的位置关系；

（Ⅱ）求直线倾斜角的取值范围；

（Ⅲ）直线能否将圆分割成弧长的比值为的两段圆弧？为什么？

Answer 1

【答案】(1) 直线与圆相交;(2) ；（3）直线不能将圆分割成弧长的比值为的两段弧.

【解析】试题分析：（Ⅰ）若，求出圆心C（4，﹣2）到直线l的距离，与半径的关系，即可判断直线l与圆C的位置关系；

（Ⅱ）直线，可得： ，利用均值不等式，即可得到直线倾斜角的取值范围；

（Ⅲ）判断 ．若直线l能将圆C分割成弧长的比值为的两段圆弧，则圆心C到直线l的距离，即可得出结论．

试题解析：

（Ⅰ）圆的圆心为,半径．

若，直线： ，即，

则圆心到直线的距离，

所以直线与圆相交．

（Ⅱ）直线的方程可化为，

直线的斜率，所以，当且仅当时等号成立．

所以斜率的取值范围是．

所以的范围为

（Ⅲ）能．由（Ⅰ）知直线恒过点，

设直线的方程为,其中．

圆心到直线的距离．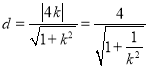

由得，又即．

若直线能将圆分割成弧长的比值为的两段圆弧，则圆心到直线的距离，

因为，所以直线不能将圆分割成弧长的比值为的两段弧．