题目内容
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为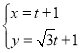 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
【答案】(1)直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
(2)![]() .
.
【解析】
(1)先写出直线![]() 的普通方程,再根据
的普通方程,再根据![]() 求出直线
求出直线![]() 的极坐标方程,对
的极坐标方程,对![]() 等式两边同乘以
等式两边同乘以![]() ,再结合
,再结合![]() 写出曲线
写出曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)先写出直线![]() 的一个参数方程,再根据参数的几何意义求解.
的一个参数方程,再根据参数的几何意义求解.
解:(1)直线![]() 的参数方程可化为
的参数方程可化为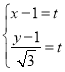 (
(![]() 为参数),
为参数),
消去![]() 可得直线
可得直线![]() 的普通方程为
的普通方程为![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
由![]() 可得
可得![]() ,即
,即![]()
∴曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
(2)由(1)可知直线![]() 的倾斜角为
的倾斜角为![]() ,
,
∴直线![]() 的倾斜角也为
的倾斜角也为![]() ,
,
又直线![]() 过点
过点![]() ,
,
∴直线![]() 的参数方程为
的参数方程为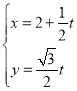 (
(![]() 为参数),
为参数),
将其代入曲线![]() 的直角坐标方程可得
的直角坐标方程可得![]() ,
,
设点![]() 对应的参数分别为
对应的参数分别为![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
∴![]()
![]()
![]() .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对于线上教育进行调查,其中男生与女生的人数之比为![]() ,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | |||
女生 | |||
合计 | 120 |
(2)从被调查中对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取2名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
参考公式:附: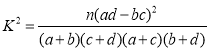
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.842 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
【题目】稠环芳香烃化合物中有不少是致癌物质,比如学生钟爱的快餐油炸食品中会产生苯并芘,它是由一个苯环和一个芘分子结合而成的稠环芳香烃类化合物,长期食用会致癌.下面是一组稠环芳香烃的结构简式和分子式:
名称 | 萘 | 蒽 | 并四苯 | … | 并n苯 |
结构简式 |
|
|
| … | … |
分子式 |
|
|
| … | … |
由此推断并十苯的分子式为________.