题目内容
【题目】已知q和n均为给定的大于1的自然数,设集合M={0,1,2,…,q﹣1},集合A={x|x=x1+x2q+…+xnqn﹣1 , xi∈M,i=1,2,…n}.
(1)当q=2,n=3时,用列举法表示集合A;
(2)设s,t∈A,s=a1+a2q+…+anqn﹣1 , t=b1+b2q+…+bnqn﹣1 , 其中ai , bi∈M,i=1,2,…,n.证明:若an<bn , 则s<t.
【答案】
(1)解:当q=2,n=3时,
M={0,1},A={x| ![]() ,xi∈M,i=1,2,3}.
,xi∈M,i=1,2,3}.
可得A={0,1,2,3,4,5,6,7}.
(2)证明:由设s,t∈A,s=a1+a2q+…+anqn﹣1,t=b1+b2q+…+bnqn﹣1,其中ai,bi∈M,i=1,2,…,n.an<bn,∴an﹣bn≤﹣1.
可得s﹣t=(a1﹣b1)+(a2﹣b2)q+…+ ![]() +
+ ![]()
≤﹣[1+q+…+qn﹣2+qn﹣1]
= ![]() <0.
<0.
∴s<t.
【解析】(1)当q=2,n=3时,M={0,1},A={x| ![]() ,xi∈M,i=1,2,3}.即可得到集合A.(2)由于ai , bi∈M,i=1,2,…,n.an<bn , 可得an﹣bn≤﹣1.由题意可得s﹣t=(a1﹣b1)+(a2﹣b2)q+…+
,xi∈M,i=1,2,3}.即可得到集合A.(2)由于ai , bi∈M,i=1,2,…,n.an<bn , 可得an﹣bn≤﹣1.由题意可得s﹣t=(a1﹣b1)+(a2﹣b2)q+…+ ![]() +
+ ![]() ≤﹣[1+q+…+qn﹣2+qn﹣1],再利用等比数列的前n项和公式即可得出.
≤﹣[1+q+…+qn﹣2+qn﹣1],再利用等比数列的前n项和公式即可得出.
【考点精析】关于本题考查的数列的前n项和,需要了解数列{an}的前n项和sn与通项an的关系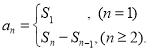 才能得出正确答案.
才能得出正确答案.

【题目】改革开放四十周年纪念币从2018年12月5日起可以开始预约![]() 通过市场调查,得到该纪念章每1枚的市场价
通过市场调查,得到该纪念章每1枚的市场价![]() 单位:元
单位:元![]() 与上市时间
与上市时间![]() 单位:天
单位:天![]() 的数据如下:
的数据如下:
上市时间x天 | 8 | 10 | 32 |
市场价y元 | 82 | 60 | 82 |
![]() 根据上表数据,从下列函数:
根据上表数据,从下列函数:![]() ;
;![]() ;
;![]() 中选取一个恰当的函数刻画改革开放四十周年纪念章的市场价y与上市时间x的变化关系并说明理由
中选取一个恰当的函数刻画改革开放四十周年纪念章的市场价y与上市时间x的变化关系并说明理由
![]() 利用你选取的函数,求改革开放四十周年纪念章市场价最低时的上市天数及最低的价格.
利用你选取的函数,求改革开放四十周年纪念章市场价最低时的上市天数及最低的价格.
【题目】苏格兰数学家纳皮尔发明了对数表,这一发明为当时的天文学家处理“大数运算”做出了巨大贡献![]() 法国著名数学家和天文学家拉普拉斯曾说过:“对数倍增了天文学家的寿命
法国著名数学家和天文学家拉普拉斯曾说过:“对数倍增了天文学家的寿命![]() ”比如在下面的部分对数表中,16,256对应的幂指数分别为4,8,幂指数和为12,而12对应的幂4096,因此
”比如在下面的部分对数表中,16,256对应的幂指数分别为4,8,幂指数和为12,而12对应的幂4096,因此![]() 根据此表,推算
根据此表,推算![]() ( )
( )
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
x | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2048 | 4096 | 8192 | 16384 | 32768 | 65536 | 131072 | 262144 | 524288 | 1048576 |
x | 21 | 22 | 23 | 24 | 25 | |||||
| 2097152 | 4194304 | 8388608 | 16777216 | 33554432 | |||||
A. 524288 B. 8388608 C. 16777216 D. 33554432

