题目内容
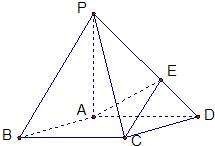
如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=a，PB=PD=| 2 |
（I）证明PA⊥平面ABCD，PB∥平面EAC；
（II）求以AC为棱，EAC与DAC为面的二面角θ的正切值．
分析：（Ⅰ）根据底面ABCD是菱形判断出∠ABC=60°，且四边长相等，在△PAB中，由PA2+AB2=2a2=PB2可推断出PA⊥AB．同样可推断出，PA⊥AD，进而根据直线与面垂直的定义判断出PA⊥平面ABCD．进而根据
=
+
.判断出
、
、
共面．，进而根据直线与面平行的判定法则，推断出PB∥平面EAC．
（Ⅱ）作EG∥PA交AD于G，由PA⊥平面ABCD．GH⊥AC于H，连接EH，进而可推断出EG⊥平面ABCD．EH⊥AC，进而可知∠EHG即为二面角θ的平面角．进而根据E是PD的中点，从而G是AD的中点，分别求得EG和GH，进而根据tanθ=
求得答案．
| PB |
| EA |
| EC |
| PB |
| EA |
| EC |
（Ⅱ）作EG∥PA交AD于G，由PA⊥平面ABCD．GH⊥AC于H，连接EH，进而可推断出EG⊥平面ABCD．EH⊥AC，进而可知∠EHG即为二面角θ的平面角．进而根据E是PD的中点，从而G是AD的中点，分别求得EG和GH，进而根据tanθ=
| EG |
| GH |
解答：（Ⅰ）证明：因为底面ABCD是菱形，∠ABC=60°，
所以AB=AD=AC=a，
在△PAB中，由PA2+AB2=2a2=PB2知PA⊥AB．
同理，PA⊥AD，所以PA⊥平面ABCD．
因为
=
+
+
=2
+
+
=(
+
)+(
+
)=
+
.
所以
、
、
共面．
又PB?平面EAC，所以PB∥平面EAC．
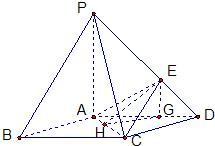
（Ⅱ）解：作EG∥PA交AD于G，由PA⊥平面ABCD．
知EG⊥平面ABCD．
作GH⊥AC于H，连接EH，则EH⊥AC，∠EHG即为二面角θ的平面角．
又E是PD的中点，从而G是AD的中点，EG=
a，AG=
a，GH=AGsin60°=
a.
所以tanθ=
=
.
所以AB=AD=AC=a，
在△PAB中，由PA2+AB2=2a2=PB2知PA⊥AB．
同理，PA⊥AD，所以PA⊥平面ABCD．
因为
| PB |
| PD |
| DC |
| CB |
| ED |
| DC |
| DA |
| ED |
| DA |
| ED |
| DC |
| EA |
| EC |
所以
| PB |
| EA |
| EC |
又PB?平面EAC，所以PB∥平面EAC．
（Ⅱ）解：作EG∥PA交AD于G，由PA⊥平面ABCD．
知EG⊥平面ABCD．
作GH⊥AC于H，连接EH，则EH⊥AC，∠EHG即为二面角θ的平面角．
又E是PD的中点，从而G是AD的中点，EG=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
所以tanθ=
| EG |
| GH |
2
| ||
| 3 |
点评：本题主要考查了直线与平面垂直的判定和二面角的问题．考查了学生综合分析问题和解决问题的能力．
练习册系列答案
相关题目
如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=a，PB=PD=
如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=a，PB=PD=
如图，在底面是菱形的四棱锥S-ABCD中，∠ABC=60°，SA=AB=a，SB=SD=
如图，在底面是菱形的四棱锥 P-ABCD中，∠ABC=60°，PA⊥平面ABCD，点E、F、G分别为CD、PD、PB的中点．PA=AD=2．
如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=2，PB=PD=2