题目内容
 如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=
如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=| 2 |
(1)证明SA⊥平面ABCD;
(2)设E是SC的中点,求证BE∥平面APC.
分析:(1)在△SAB中,利用勾股定理可证SA⊥AB,同理可证SA⊥AD,利用线面垂直的判定定理即可证明SA⊥平面ABCD;
(2)连BD,设BD与AC交于O,连OP,取SP的中点M,易证平面BME∥平面PAC,从而可得BE∥平面APC.
(2)连BD,设BD与AC交于O,连OP,取SP的中点M,易证平面BME∥平面PAC,从而可得BE∥平面APC.
解答: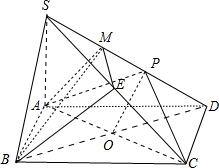 证明:(1)证明:因为底面ABCD是菱形,∠ABC=60°,
证明:(1)证明:因为底面ABCD是菱形,∠ABC=60°,
所以AB=AC=AD=a
在△SAB中,由SA2+AB2=2a2=SB2,知SA⊥AB,
同理SA⊥AD.
所以SA⊥平面ABCD.…(6分)
(2)连BD,设BD与AC交于O,连OP,O显然平分BD,
取SP的中点M,
∵SD=3PD,
∴SM=MP=PD.…(8分)
因此,BM∥OP,又E是SC的中点,故EM∥CP.
从而平面BME∥平面PAC.
又BE?平面BME,故BE∥平面PAC.…(12分)
 证明:(1)证明:因为底面ABCD是菱形,∠ABC=60°,
证明:(1)证明:因为底面ABCD是菱形,∠ABC=60°,所以AB=AC=AD=a
在△SAB中,由SA2+AB2=2a2=SB2,知SA⊥AB,
同理SA⊥AD.
所以SA⊥平面ABCD.…(6分)
(2)连BD,设BD与AC交于O,连OP,O显然平分BD,
取SP的中点M,
∵SD=3PD,
∴SM=MP=PD.…(8分)
因此,BM∥OP,又E是SC的中点,故EM∥CP.
从而平面BME∥平面PAC.
又BE?平面BME,故BE∥平面PAC.…(12分)
点评:本题考查直线与平面垂直的判定,考查面面垂直的性质,着重考查推理证明的能力,属于中档题

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.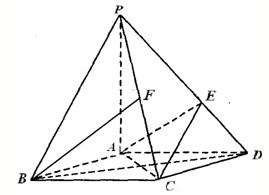 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2