题目内容
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=| 2 |
(Ⅰ)求二面角E-AC-D的大小:
(Ⅱ)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
分析:(1)由已知中,∠ABC=60°,PA=AC=a,PB=PD=
a,由勾股定理可得PA⊥AB,PA⊥AD,由线面垂直的判定定理可得PA⊥平面ABCD;
(2)设F为PC中点,取PE中点G,连接FG、BG,设AC、BD交于O,连接OE,由三角形中位线定理可得GF∥EC,OE∥BP,根据面面平行的判定定理可得平面BGF∥平面AEC,由面面平行的性质可得BF∥平面AEC.
| 2 |
(2)设F为PC中点,取PE中点G,连接FG、BG,设AC、BD交于O,连接OE,由三角形中位线定理可得GF∥EC,OE∥BP,根据面面平行的判定定理可得平面BGF∥平面AEC,由面面平行的性质可得BF∥平面AEC.
解答: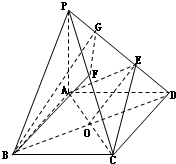 解:(1)由ABCD是菱形,且∠ABC=60°得
解:(1)由ABCD是菱形,且∠ABC=60°得
AB=BC=CD=AD=AC=PA=a
由PB=PD=
a
得PB2=PA2+AB2,PD2=PA2+AD2
∴PA⊥AB,PA⊥AD
∴PA⊥平面ABCD
(2)设F为PC中点,取PE中点G,连接FG、BG
设AC、BD交于O,连接OE
由PG=GE,PF=FC得GF∥EC
由DO=OB,DE=EG得OE∥BG
∴平面BGF∥平面AEC
∴BF∥平面AEC
∴F是PC中点时,BF∥平面AEC
 解:(1)由ABCD是菱形,且∠ABC=60°得
解:(1)由ABCD是菱形,且∠ABC=60°得AB=BC=CD=AD=AC=PA=a
由PB=PD=
| 2 |
得PB2=PA2+AB2,PD2=PA2+AD2
∴PA⊥AB,PA⊥AD
∴PA⊥平面ABCD
(2)设F为PC中点,取PE中点G,连接FG、BG
设AC、BD交于O,连接OE
由PG=GE,PF=FC得GF∥EC
由DO=OB,DE=EG得OE∥BG
∴平面BGF∥平面AEC
∴BF∥平面AEC
∴F是PC中点时,BF∥平面AEC
点评:本题考查的知识点是直线与平面垂直的判定,直线与平面平行的判定,其中(1)的关键是利用勾股定理证得PA⊥AB,PA⊥AD,(2)的关键是证得BGF∥平面AEC.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=
如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD= 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.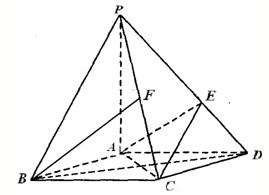 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2