题目内容
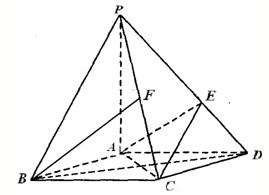 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2| 2 |
(Ⅰ)求证:PC⊥BD;
(Ⅱ)求BF与平面ABCD所成角的大小;
(Ⅲ)若点E在棱PD上,当
| PE |
| PD |
| π |
| 6 |
分析:本题是考查证线线垂直,求线面角与二面的方法,由题设条件,可令BD与AC的交点为O,可证得P0垂直于底面ABCD,由菱形的性质,AC与BD互相垂直,本题的图象中出现了同一点出发的三条线段两两垂直,故可以建立空间坐标系用向量法求解,以O为坐标原点,OB方向为X轴,OC方向为Y轴,OP方向为Z轴建立空间坐标系,
(I)求出PC与BD两线对应的方向向量,利用内积为0证明线线垂直;
(II)求出直线BF的方向向量,与平面ABCD的法向量,利用公式求线面角;
(III)先设
=t,用t表示出两个平面的法向量,由于两平面的夹角为
,由此建立关于t的方程求出t的值,即可得到点E的位置.
(I)求出PC与BD两线对应的方向向量,利用内积为0证明线线垂直;
(II)求出直线BF的方向向量,与平面ABCD的法向量,利用公式求线面角;
(III)先设
| PE |
| PD |
| π |
| 6 |
解答:解:令AC与BD的交点为O,由于底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,可得AO=1,BO=
又PB=PD=2
,在等腰三角形PBD中,由勾股定理可解得P0=
故有PA2+AO2=5=PO2,故有PO⊥AC,即有PO,AC,BD三线两两垂直,由此,可以O为坐标原点,,OB方向为X轴,OC方向为Y轴,OP方向为Z轴建立空间坐标系,故有A(0,-1,0),B(
,0,0),C(0,1,0),D(-
,0,0),P(0,0,
)
(I)
=(0,1,-
),
=(-2
,0,0),因为
•
=0,故有PC⊥BD;
(II)由前证易得P0⊥面ABCD,故
即为平面ABCD的法向量,其坐标为(0,0,
)
又F是PC的中点,故其坐标为(0,
,
),所以
=(-
,
,
)
设线面角为θ,故有sinθ=|
|=
=
,故有θ=arcsin
,即所求的线面角为arcsin
(III)连接OE,由于AC⊥面PBD,故可得∠EOD即是二面角E-AC-D的平面角,
设
=t,由PE=tPD,可以得出,ED=(1-t)PD,作EM垂直OD于M,故点E到底面的距离是EM=(1-t)
,,OM=t
又二面角E-AC-D的大小为
,可得tan
=
=
=
,即有t=(1-t)
,解得t=
=
| 3 |
又PB=PD=2
| 2 |
| 5 |
故有PA2+AO2=5=PO2,故有PO⊥AC,即有PO,AC,BD三线两两垂直,由此,可以O为坐标原点,,OB方向为X轴,OC方向为Y轴,OP方向为Z轴建立空间坐标系,故有A(0,-1,0),B(
| 3 |
| 3 |
| 5 |
(I)
| PC |
| 5 |
| BD |
| 3 |
| PC |
| BD |
(II)由前证易得P0⊥面ABCD,故
| OP |
| 5 |
又F是PC的中点,故其坐标为(0,
| 1 |
| 2 |
| ||
| 2 |
| BF |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
设线面角为θ,故有sinθ=|
| ||||
|
|
| ||||||
|
| ||
| 6 |
| ||
| 6 |
| ||
| 6 |
(III)连接OE,由于AC⊥面PBD,故可得∠EOD即是二面角E-AC-D的平面角,
设
| PE |
| PD |
| 5 |
| 3 |
又二面角E-AC-D的大小为
| π |
| 6 |
| π |
| 6 |
| EM |
| OM |
(1-t)
| ||
t
|
| ||
| 3 |
| 5 |
| ||
1+
|
5-
| ||
| 2 |
点评:本题考查与二面角有关的立体几何综合题,由于本题中出现了同一点出发的三条两两垂直的直线,适合建立坐标系,故采用了向量法证明线线垂直,求线面角,在第三问中,由于本题中几何体的结构特点,易得出二面角的平面角,故采用了传统的立体几何的方法研究二面角为
时
的比,解题时要根据题设条件灵活选用方法,以达到简化解题的目的.
| π |
| 6 |
| PE |
| PD |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=
如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD= 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.