题目内容
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=| 2 |
(Ⅰ)证明PA⊥平面ABCD;
(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小;
(Ⅲ)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
分析:(I)证明PA⊥AB,PA⊥AD,AB、AD是平面ABCD内的两条相交直线,即可证明PA⊥平面ABCD;
(II)求以AC为棱,作EG∥PA交AD于G,作GH⊥AC于H,连接EH,说明∠EHG即为二面角θ的平面角,解三角形求EAC与DAC为面的二面角θ的大小;
(Ⅲ)证法一F是棱PC的中点,连接BM、BD,设BD∩AC=O,利用平面BFM∥平面AEC,证明使BF∥平面AEC.
证法二建立空间直角坐标系,求出
、
、
共面,BF?平面AEC,所以当F是棱PC的中点时,BF∥平面AEC.
还可以通过向量表示,和转化得到
、
、
是共面向量,BF?平面ABC,从而BF∥平面AEC.
(II)求以AC为棱,作EG∥PA交AD于G,作GH⊥AC于H,连接EH,说明∠EHG即为二面角θ的平面角,解三角形求EAC与DAC为面的二面角θ的大小;
(Ⅲ)证法一F是棱PC的中点,连接BM、BD,设BD∩AC=O,利用平面BFM∥平面AEC,证明使BF∥平面AEC.
证法二建立空间直角坐标系,求出
| BF |
| AC |
| AE |
还可以通过向量表示,和转化得到
| BF |
| AC |
| AE |
解答: 解:(Ⅰ)证明因为底面ABCD是菱形,∠ABC=60°,
解:(Ⅰ)证明因为底面ABCD是菱形,∠ABC=60°,
所以AB=AD=AC=a,在△PAB中,
由PA2+AB2=2a2=PB2知PA⊥AB.
同理,PA⊥AD,所以PA⊥平面ABCD.
(Ⅱ)解:作EG∥PA交AD于G,
由PA⊥平面ABCD.
知EG⊥平面ABCD.作GH⊥AC于H,连接EH,
则EH⊥AC,∠EHG即为二面角θ的平面角.
又PE:ED=2:1,所以EG=
a,AG=
a,GH=AGsin60°=
a.
从而tanθ=
=
,θ=30°.
(Ⅲ)解法一以A为坐标原点,直线AD、AP分别为y轴、z轴,
过A点垂直平面PAD的直线为x轴,建立空间直角坐标系如图.
由题设条件,相关各点的坐标分别为A(0,0,0),B(
a,-
a,0),C(
a,
a,0).D(0,a,0),P(0,0,a),E(0,
a,
a).
所以
=(0,
a,
a),
=(
a,
a,0).
=(0,0,a),
=(
a,
a,-a).
=(-
a,
a,a).
设点F是棱PC上的点,
=λ
=(
aλ,
aλ,-aλ),其中0<λ<1,
则
=
+
=(-
a,
a,a)+(
aλ,
aλ,-aλ)=(
a(λ-1),
a(1+λ),a(1-λ)).
令
=λ1
+λ2
得
即
解得λ=
,λ1=-
,λ2=
.即λ=
时,
=-
+
.
亦即,F是PC的中点时,
、
、
共面.
又BF?平面AEC,所以当F是棱PC的中点时,BF∥平面AEC.
解法二:当F是棱PC的中点时,BF∥平面AEC,证明如下,
证法一:取PE的中点M,连接FM,则FM∥CE.①
由EM=
PE=ED,知E是MD的中点.
连接BM、BD,设BD∩AC=O,则O为BD的中点.
所以BM∥OE.②
由①、②知,平面BFM∥平面AEC.
又BF?平面BFM,所以BF∥平面AEC.
证法二:
因为
=
+
=
+
(
+
)=
+
+
=
+
(
-
)+
(
-
)=
-
.
所以
、
、
共面.
又BF?平面ABC,从而BF∥平面AEC.
 解:(Ⅰ)证明因为底面ABCD是菱形,∠ABC=60°,
解:(Ⅰ)证明因为底面ABCD是菱形,∠ABC=60°,所以AB=AD=AC=a,在△PAB中,
由PA2+AB2=2a2=PB2知PA⊥AB.
同理,PA⊥AD,所以PA⊥平面ABCD.
(Ⅱ)解:作EG∥PA交AD于G,
由PA⊥平面ABCD.
知EG⊥平面ABCD.作GH⊥AC于H,连接EH,
则EH⊥AC,∠EHG即为二面角θ的平面角.
又PE:ED=2:1,所以EG=
| 1 |
| 3 |
| 2 |
| 3 |
| ||
| 3 |
从而tanθ=
| EG |
| GH |
| ||
| 3 |
(Ⅲ)解法一以A为坐标原点,直线AD、AP分别为y轴、z轴,

过A点垂直平面PAD的直线为x轴,建立空间直角坐标系如图.
由题设条件,相关各点的坐标分别为A(0,0,0),B(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
所以
| AE |
| 2 |
| 3 |
| 1 |
| 3 |
| AC |
| ||
| 2 |
| 1 |
| 2 |
| AP |
| PC |
| ||
| 2 |
| 1 |
| 2 |
| BP |
| ||
| 2 |
| 1 |
| 2 |
设点F是棱PC上的点,
| PF |
| PC |
| ||
| 2 |
| 1 |
| 2 |
则
| BF |
| BP |
| PF |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
令
| BF |
| AC |
| AE |
|
|
解得λ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| BF |
| 1 |
| 2 |
| AC |
| 3 |
| 2 |
| AE |
亦即,F是PC的中点时,
| BF |
| AC |
| AE |
又BF?平面AEC,所以当F是棱PC的中点时,BF∥平面AEC.
解法二:当F是棱PC的中点时,BF∥平面AEC,证明如下,
证法一:取PE的中点M,连接FM,则FM∥CE.①

由EM=
| 1 |
| 2 |
连接BM、BD,设BD∩AC=O,则O为BD的中点.
所以BM∥OE.②
由①、②知,平面BFM∥平面AEC.
又BF?平面BFM,所以BF∥平面AEC.
证法二:
因为
| BF |
| BC |
| 1 |
| 2 |
| CP |
| AD |
| 1 |
| 2 |
| CD |
| DP |
| AD |
| 1 |
| 2 |
| CD |
| 3 |
| 2 |
| DE |
| AD |
| 1 |
| 2 |
| AD |
| AC |
| 3 |
| 2 |
| AE |
| AD |
| 3 |
| 2 |
| AE |
| 1 |
| 2 |
| AC |
所以
| BF |
| AE |
| AC |
又BF?平面ABC,从而BF∥平面AEC.
点评:本题考查直线与平面平行的判定,二面角的求法,直线与平面垂直的判定,考查空间想象能力,逻辑思维能力,计算能力,转化思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=
如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD= 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.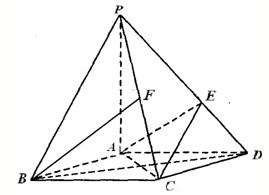 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2