题目内容
15.若函数y=loga(x+3)-1(a>0,且a≠1)的图象恒过点A(m,n),则函数f(x)=${log}_{\frac{1}{2}}$(nx2-mx+3)的单调递增区间[1,3),.分析 根据对数函数的性质求出定点坐标,确定m,n,利用换元法,结合复合函数单调性之间的进行求解即可.
解答 解:由x+3=1得x=-2,此时y=loga1-1=-1,
即函数过定点A(-2,-1),即m=-2,n=-1,
即f(x)=${log}_{\frac{1}{2}}$(nx2-mx+3)=${log}_{\frac{1}{2}}$(-x2+2x+3)
设t=-x2+2x+3,由t=-x2+2x+3>0得-1<x<3,且当x∈(-1,1]时,函数t=-x2+2x+3递增,
当x∈[1,3)时,函数t=-x2+2x+3递减,
则函数y=${log}_{\frac{1}{2}}$t为减函数,
要求f(x)=${log}_{\frac{1}{2}}$(nx2-mx+3)的单调递增区间,即求t=-x2+2x+3的递减区间,
即x∈[1,3),
故函数f(x)的递增区间为[1,3),
故答案为:[1,3).
点评 本题主要考查函数单调区间的求解,利用复合函数单调性之间的关系以及对数函数的性质是解决本题的关键.

练习册系列答案
相关题目
1.已知O为坐标原点,A,B两点的坐标均满足不等式组$\left\{\begin{array}{l}{x-3y+1≤0}\\{x+y-3≤0}\\{x-1≥0}\end{array}\right.$则tan∠AOB的最大值等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{9}{4}$ |
10.定义[X]表示不超过X的最大整数.设n∈N*,且M=(n+1)2+n-[$\sqrt{(n+1)^{2}+n+1}$]2,则下列不等式恒成立的是( )
| A. | M2≥2n+1 | B. | 当n≥2时,2M≥4n-2 | C. | M2≥2n+1 | D. | 当n≥3时,2M≥2n+2 |
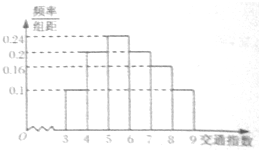 交通指数是交通拥堵指数的简称,是综合反映道路间畅通或拥堵的概念.记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从郑州市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图 所示:
交通指数是交通拥堵指数的简称,是综合反映道路间畅通或拥堵的概念.记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从郑州市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图 所示: 如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.
如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.