题目内容
【题目】已知椭圆![]() 上一点
上一点![]() 与椭圆右焦点的连线垂直于
与椭圆右焦点的连线垂直于![]() 轴,过椭圆
轴,过椭圆![]() 上一点
上一点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(
两点(![]() 均不在坐标轴上),设
均不在坐标轴上),设![]() 为坐标原点,过
为坐标原点,过![]() 的射线
的射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() .
.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)当![]() 为
为![]() 时,若四边形
时,若四边形![]() 的面积为12,试求直线
的面积为12,试求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题意可知![]() 且
且![]() ,从而求出椭圆
,从而求出椭圆![]() 的方程,再把点
的方程,再把点![]() 再把代入椭圆方程,即可求出
再把代入椭圆方程,即可求出![]() 的值;
的值;
(2)设![]() ,由直线过点
,由直线过点![]() 知
知![]() ①,分别联立直线
①,分别联立直线![]() 与椭圆
与椭圆![]() 和椭圆
和椭圆![]() 的方程,利用韦达定理得到所以
的方程,利用韦达定理得到所以![]() ,化简得
,化简得![]() ②,由①②即可解得
②,由①②即可解得![]() 和
和![]() 的值,从而求出直线
的值,从而求出直线![]() 的方程.
的方程.
解:(1)椭圆![]() 的右焦点坐标为(1,0),且
的右焦点坐标为(1,0),且![]() ,
,
又![]() ,
,
解得:![]() ,
,
所以椭圆![]() 的方程为:
的方程为:![]() ,
,
设![]() ,则
,则![]() ,
,
由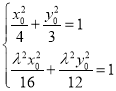 得:
得:![]() ,
,
又![]() ,故
,故![]() ;
;
(2)设![]() ,
,
由直线过点![]() 知
知![]() ①,
①,
由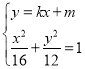 得,
得,![]() ,
,
有![]() ,
,
且![]() ,
,
由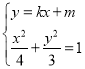 得,
得,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
化简得![]() ,得
,得![]() ②,
②,
由①②解得:![]() ,
,
所以直线![]() 的方程为:
的方程为:![]() .
.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】某学生社团对![]() 年元宵节当天游览磁器口古镇景区的游客满意度抽样调查,从当日
年元宵节当天游览磁器口古镇景区的游客满意度抽样调查,从当日![]() 万名游客中随机抽取
万名游客中随机抽取![]() 人进行统计,结果如下图的频率分布表和频率分布直方图:
人进行统计,结果如下图的频率分布表和频率分布直方图:
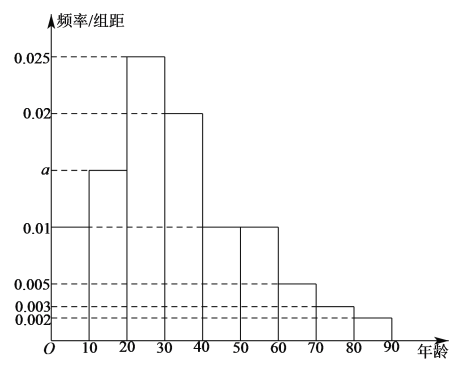
年龄 | 频数 | 频率 | 满意 | 不满意 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
|
|
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)利用频率分布直方图,估算游客的平均年龄和年龄的中位数;
(3)称年龄不低于![]() 岁的人群为“安逸人群”,完成
岁的人群为“安逸人群”,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为游客的满意度与“安逸人群”人数相关.
的把握认为游客的满意度与“安逸人群”人数相关.
|
| 合计 | |
满意 | |||
不满意 | |||
合计 |
参考公式: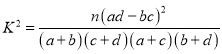 ,其中
,其中![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
