题目内容
(本题满分16分) 已知椭圆 :
: 的离心率为
的离心率为 ,
, 分别为椭圆
分别为椭圆 的左、右焦点,若椭圆
的左、右焦点,若椭圆 的焦距为2.
的焦距为2.
⑴求椭圆 的方程;
的方程;
⑵设 为椭圆上任意一点,以
为椭圆上任意一点,以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,当圆
,当圆 与椭圆的右准线
与椭圆的右准线 有公共点时,求△
有公共点时,求△ 面积的最大值.
面积的最大值.
【答案】
⑴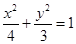 .⑵
.⑵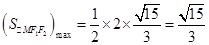 .
.
【解析】(1)由离心率和b值,不难求出a,从而方程易求。
(2)在(1)的基础上,可知由于圆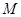 与
与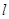 有公共点,所以
有公共点,所以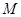 到
到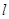 的距离
的距离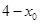 小于或等于圆的半径
小于或等于圆的半径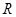 .因为
.因为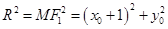 ,所以
,所以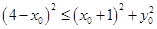 ,
,
即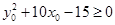 .然后再借助椭圆方程,消y0转化为
.然后再借助椭圆方程,消y0转化为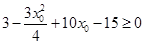 求解即可。
求解即可。
解:⑴因为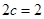 ,且
,且 ,所以
,所以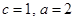 .……………………………………2分
.……………………………………2分
所以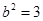 .………………………………………………………………………………4分
.………………………………………………………………………………4分
所以椭圆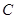 的方程为
的方程为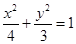 .……………………………………………………6分
.……………………………………………………6分
⑵设点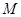 的坐标为
的坐标为 ,则
,则 .
.
因为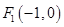 ,
,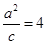 ,所以直线
,所以直线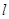 的方程为
的方程为 .………………………………8分
.………………………………8分
由于圆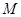 与
与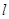 有公共点,所以
有公共点,所以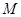 到
到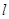 的距离
的距离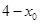 小于或等于圆的半径
小于或等于圆的半径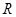 .
.
因为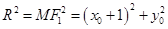 ,所以
,所以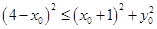 ,………………10分
,………………10分
即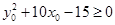 .
.
又因为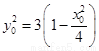 ,所以
,所以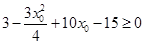 .…………………………12分
.…………………………12分
解得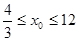 ,又
,又 ,∴
,∴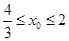 .……………………………………14分
.……………………………………14分
当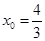 时,
时,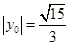 ,所以
,所以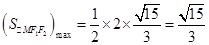 .…………16分
.…………16分

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在