题目内容
（本题满分16分）已知数列
的前
项和为
，且
．数列
中，
，
．（1）求数列的通项公式；（2）若存在常数
使数列
是等比数列，求数列的通项公式；（3）求证：①
；②
．
(Ⅰ) 
(Ⅱ) 
（Ⅲ）略
解析:
：（Ⅰ）
时，
，
时，
， -------2分
且时也适合此式，故数列
的通项公式是；
------3分
（Ⅱ）依题意，时，
，
∴
，又
，-----6分
∴
是以2为首项，2为公比的等比数列，即存在常数
=2使数列
是等比数列
，即. -------8分
（Ⅲ） ①
所以
对一切自然数
都成立10分
②由得
设
则S
13分
所以
． -----16分
练习册系列答案
全能测控期末小状元系列答案
相关题目
，且对任意
，有
.
；
在区间（0，1）上为单调函数，求实
数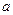
的取值范围.
的零点个数？(提示
)
为实常数）．
时，求函数
在
上的最小值；
在区间
上有解，求实数
的取值范围；
）
：
的离心率为
，
分别为椭圆
为椭圆上任意一点，以
为半径作圆
有公共点时，求△
面积的最大值．
是定义在
上的偶函数，且当
时，
。
及
的值；
上的解析式；
的方程
有四个不同的实数解，求实数
的取值范围。