题目内容
本题满分16分)已知圆内接四边形ABCD的边长分别为AB = 2,BC = 6,CD = DA = 4;求四边形ABCD的面积.
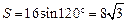
解析解:如图,连结BD,则有四边形ABCD的面积,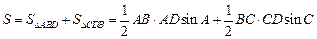 .
. ∵A+C = 180°,∴ sin A =" sin" C;
∵A+C = 180°,∴ sin A =" sin" C;
∴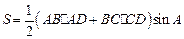 ;
;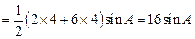 .
.
又由余弦定理,
在△ABD中,BD 2 = AB 2+AD 2-2AB · ADcosA =22+42-2×2×4cos A= 20-16cos A;
在△CDB中,BD 2 = CB 2+CD 2-2CB · CDcosC = 62+42-2×6×4cos C = 52-48cosC;
∴ 20-16cosA= 52-48cosC;
∵ cosC = -cosA,∴ 64cos A =-32,∴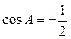 ,∴A = 120°,
,∴A = 120°,
∴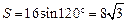 .
.

练习册系列答案
相关题目
 ,且对任意
,且对任意 ,有
,有 .
. ;
; 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数 的取值范围.
的取值范围. 的零点个数?(提示
的零点个数?(提示 )
) :
: 的离心率为
的离心率为 ,
, 分别为椭圆
分别为椭圆 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆 有公共点时,求△
有公共点时,求△ 面积的最大值.
面积的最大值.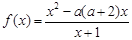 (
( .
.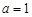 时,求
时,求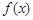 在点
在点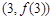 处的切线方程;
处的切线方程;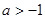 时,解关于
时,解关于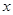 的不等式
的不等式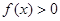 ;
;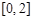 上的最小值..
上的最小值..