题目内容
设等比数列{an}的前n项和为Sn,已知an + 1 = 2Sn + 2 (n∈N*).
(1)求数列{an}的通项公式;
(2)在an与an + 1之间插入n个数,使这n + 2个数组成一个公差为dn的等差数列.
①在数列{dn}中是否存在三项dm,dk,dp (其中m,k,p成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
②求证: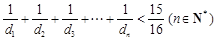 .
.
(1)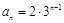 (2)不存在(证明见解析) (3)证明见解析
(2)不存在(证明见解析) (3)证明见解析
解析试题分析:(1)利用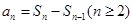 和等比数列的定义即可得出;
和等比数列的定义即可得出;
(2)利用等差数列的通向公式即可得出;
①假设在数列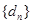 中存在三项
中存在三项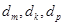 (其中
(其中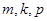 是等差数列)成等比数列,利用等差数列和等比数列的定义及其反证法即可得出;
是等差数列)成等比数列,利用等差数列和等比数列的定义及其反证法即可得出;
②利用(2)的结论、“错位相减法”和等比数列的前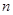 和公式即可得出.
和公式即可得出.
试题解析:(1)解:由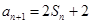 ,得:
,得: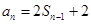
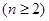
两式相减:
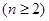
∵数列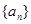 是等比数列,∴
是等比数列,∴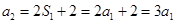 ,故
,故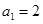
因此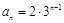 .
.
(2)解:由题意 ,即
,即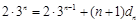 ,故
,故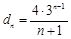
①假设在数列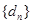 中存在三项
中存在三项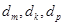 (其中
(其中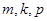 是等差数列)成等比数列
是等差数列)成等比数列
则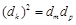 ,即:
,即: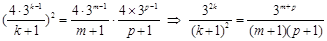 (*)
(*)
∵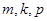 成等差数列,∴
成等差数列,∴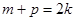
(*)可以化为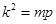 ,故
,故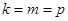 ,这与题设矛盾
,这与题设矛盾
∴在数列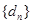 中不存在三项
中不存在三项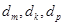 (其中
(其中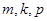 是等差数列)成等比数列.
是等差数列)成等比数列.
②令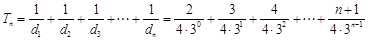
则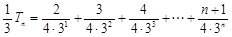
两式相减得: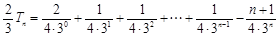
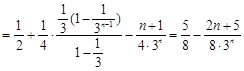
∴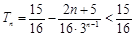 .
.
考点:等差数列和等比数列的性质;错位相减法求和.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 满足
满足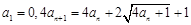 ,令
,令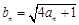 .
. 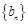 是否为等差数列?并说明理由;
是否为等差数列?并说明理由;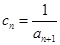 ,求
,求 前
前 项的和
项的和 ;
;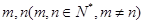 使得
使得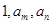 三数成等比数列?
三数成等比数列? 的前
的前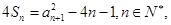 且
且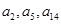 构成等比数列.(1) 证明:
构成等比数列.(1) 证明: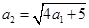 ;(2) 求数列
;(2) 求数列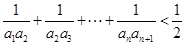 .
.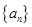 中,
中,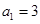 ,前
,前 项和
项和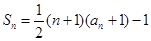 .
.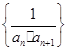 的前
的前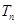 ,是否存在实数
,是否存在实数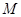 ,使得
,使得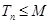 对一切正整数
对一切正整数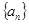 ( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.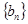 是等差数列;
是等差数列;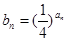 ,求证:数列{bn}是等比数列,并求其前n项和Tn.
,求证:数列{bn}是等比数列,并求其前n项和Tn.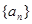 的前
的前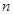 项和为
项和为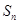 ,且
,且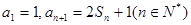 ,数列
,数列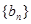 为等差数列,且
为等差数列,且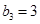 ,
, .
.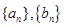 的通项公式;
的通项公式;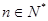 ,
,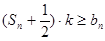 恒成立,求实数
恒成立,求实数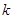 的取值范围.
的取值范围.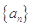 的首项
的首项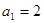 ,且对任意
,且对任意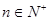 都有
都有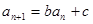 (其中
(其中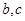 为常数).
为常数). 为等差数列,且
为等差数列,且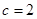 ,求
,求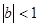 ,从数列
,从数列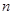 项和
项和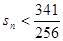 成立的
成立的 是4和16的等差中项,则
是4和16的等差中项,则