题目内容
设无穷等差数列{an}的前n项和为Sn.(Ⅰ)若首项![]() ,公差
,公差![]() ,求满足
,求满足![]() 的正整数k;
的正整数k;
(Ⅱ)求所有的无穷等差数列{an},使得对于一切正整数k都有![]() 成立.
成立.
答案:
解析:
解析:
| 解:(I)当
由 即 (II)设数列{an}的公差为d,则在
(1) (2) 由(1)得 当 若 若 当 若 若 综上,共有3个满足条件的无穷等差数列: ①{an} : an=0,即0,0,0,…; ②{an} : an=1,即1,1,1,…; ③{an} : an=2n-1,即1,3,5,…,
|

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
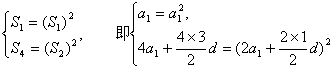
 ,公差d=1.求满足
,公差d=1.求满足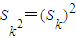 的正整数k;
的正整数k;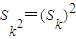 成立.
成立.