题目内容
设无穷等差数列{an}的前n项和为Sn,求所有的无穷等差数列{an},使得对于一切正整数k都有Sk3=(Sk)3成立.
分析:先由k=1,k=2时,确定首项和公差,再验证每一组解是否符合题意,从而可以找到符合题意的数列
解答:解:若等差数列{an}满足Sk3=(Sk)3
则当k=1时,有s1=s13,∴a1=0或a1=1或a1=-1
当k=2时,有s8=s2 3,即8a1+
d=(2a1+d)3
(1)当a1=0时,代入上式得d=0或d=2
或d=-2
①当a1=0,d=0时,an=0,Sn=0
满足Sk3=(Sk)3
此时,数列{an}为:0,0,0…
②当a1=0,d=2
时,an=2
(n-1),Sn=
=
n(n-1)
S27≠(S3)3
∴不满足题意
③当a1=0,d=-2
时,an=-2
(n-1),Sn=
= -
n(n-1)
S27≠(S3)3
∴不满足题意
(2)当a1=1时,代入上式得d=0或d=2或d=-8
①当a1=1,d=0时,an=1,Sn=n
满足Sk3=(Sk)3
此时,数列{an}为:1,1,1…
②当a1=1,d=2时,an=2n-1,Sn=n2
满足Sk3=(Sk)3
此时,数列{an}为:1,3,5…
③当a1=1,d=-8时,an=-8n+9,Sn=n(5-4n)
S27≠(S3)3
∴不满足题意
(3)当a1=-1时,代入上式得d=0或d=-2或d=8
①当a1=-1,d=0时,an=-1,Sn=-n
满足Sk3=(Sk)3
此时,数列{an}为:-1,-1,-1…
②当a1=-1,d=-2时,an=-2n+1,Sn=-n2
满足Sk3=(Sk)3
此时,数列{an}为:-1,-3,-5…
③当a1=-1,d=8时,an=8n-9,Sn=n(4n-5)
S27≠(S3)3
∴不满足题意
∴满足题意的等差数列{an}有:
①0,0,0…
②1,1,1…
③1,3,5…
④-1,-1,-1…
⑤-1,-3,-5…
则当k=1时,有s1=s13,∴a1=0或a1=1或a1=-1
当k=2时,有s8=s2 3,即8a1+
| 8×7 |
| 2 |
(1)当a1=0时,代入上式得d=0或d=2
| 7 |
| 7 |
①当a1=0,d=0时,an=0,Sn=0
满足Sk3=(Sk)3
此时,数列{an}为:0,0,0…
②当a1=0,d=2
| 7 |
| 7 |
2
| ||
| 2 |
| 7 |
S27≠(S3)3
∴不满足题意
③当a1=0,d=-2
| 7 |
| 7 |
-2
| ||
| 2 |
| 7 |
S27≠(S3)3
∴不满足题意
(2)当a1=1时,代入上式得d=0或d=2或d=-8
①当a1=1,d=0时,an=1,Sn=n
满足Sk3=(Sk)3
此时,数列{an}为:1,1,1…
②当a1=1,d=2时,an=2n-1,Sn=n2
满足Sk3=(Sk)3
此时,数列{an}为:1,3,5…
③当a1=1,d=-8时,an=-8n+9,Sn=n(5-4n)
S27≠(S3)3
∴不满足题意
(3)当a1=-1时,代入上式得d=0或d=-2或d=8
①当a1=-1,d=0时,an=-1,Sn=-n
满足Sk3=(Sk)3
此时,数列{an}为:-1,-1,-1…
②当a1=-1,d=-2时,an=-2n+1,Sn=-n2
满足Sk3=(Sk)3
此时,数列{an}为:-1,-3,-5…
③当a1=-1,d=8时,an=8n-9,Sn=n(4n-5)
S27≠(S3)3
∴不满足题意
∴满足题意的等差数列{an}有:
①0,0,0…
②1,1,1…
③1,3,5…
④-1,-1,-1…
⑤-1,-3,-5…
点评:本题考查等差数列通项公式和前n项和的计算,要注意分类讨论.属中档题

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 ,公差d=1.求满足
,公差d=1.求满足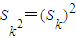 的正整数k;
的正整数k;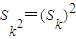 成立.
成立.