题目内容
设无穷等差数列{an}的前n项和为Sn.
(1)若首项a1=
,公差d=1,满足Sk2=(Sk)2的正整数k=
(2)对于一切正整数k都有Sk2=(Sk)2成立的所有的无穷等差数列是
(1)若首项a1=
| 3 | 2 |
4
4
;(2)对于一切正整数k都有Sk2=(Sk)2成立的所有的无穷等差数列是
an=0或an=1或an=2n-1
an=0或an=1或an=2n-1
.分析:(1)由首项a1,公差d的值,利用等差数列的求和公式分别表示出Sk2与Sk,代入Sk2=(Sk)2中化简后,得到关于k的方程,根据k为正整数,求出方程的解即可得到满足题意k的值;
(2)设无穷等差数列{an}的公差为d,取k=1和k=2,根据Sk2=(Sk)2列出方程组,利用等差数列的通项公式及求和公式变形后,得到关于a1与d的方程组,分别记作①和②,由①解得a1的值为0或1,分两种情况考虑:(i)当a1=0时,代入②求出d的值为0或6,经检验得到d=6不合题意,舍去,故d=0满足题意;当a1=1时,代入②求出d的值为0或2,经检验都满足题意,综上,得到所有满足题意的无穷等差数列.
(2)设无穷等差数列{an}的公差为d,取k=1和k=2,根据Sk2=(Sk)2列出方程组,利用等差数列的通项公式及求和公式变形后,得到关于a1与d的方程组,分别记作①和②,由①解得a1的值为0或1,分两种情况考虑:(i)当a1=0时,代入②求出d的值为0或6,经检验得到d=6不合题意,舍去,故d=0满足题意;当a1=1时,代入②求出d的值为0或2,经检验都满足题意,综上,得到所有满足题意的无穷等差数列.
解答:解:(1)∵首项a1=
,公差d=1.
∴Sn=na1+
d=
+
=
n2+n,
由Sk2=(Sk)2得:
(k2)2+k2=(
k2+k)2,
即
k4-k3=0,
∵k是正整数,∴k=4;…(5分)
(Ⅱ)设无穷等差数列{an}的公差为d,
则在Sk2=(Sk)2中分别取k=1,和k=2得:
,即
,
由①得:a1=0或a1=1,
(i)当a1=0时,代入②得:d=0或d=6,
若a1=0,d=0,则本题成立;
若a1=0,d=6,则an=6(n-1),
由S3=18,(S3)2=324,S9=216知:S9≠(S3)2,故所得数列不符合题意;
(ii)当a1=1时,代入②得4+6d=(2+d)2,解得:d=0或d=2,
若a=1,d=0则an=1,Sn=n,从而Sk2=(Sk)2成立;
若a1=1,d=2,则an=2n-1,Sn=n2,从而Sk2=(Sk)2成立,
综上所述,只有3个满足条件的无穷等差数列,分别为an=0或an=1或an=2n-1.
故答案为:(1)4;(2)an=0或an=1或an=2n-1
| 3 |
| 2 |
∴Sn=na1+
| n(n-1) |
| 2 |
| 3n |
| 2 |
| n(n-1) |
| 2 |
| 1 |
| 2 |
由Sk2=(Sk)2得:
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 4 |
∵k是正整数,∴k=4;…(5分)
(Ⅱ)设无穷等差数列{an}的公差为d,
则在Sk2=(Sk)2中分别取k=1,和k=2得:
|
|
由①得:a1=0或a1=1,
(i)当a1=0时,代入②得:d=0或d=6,
若a1=0,d=0,则本题成立;
若a1=0,d=6,则an=6(n-1),
由S3=18,(S3)2=324,S9=216知:S9≠(S3)2,故所得数列不符合题意;
(ii)当a1=1时,代入②得4+6d=(2+d)2,解得:d=0或d=2,
若a=1,d=0则an=1,Sn=n,从而Sk2=(Sk)2成立;
若a1=1,d=2,则an=2n-1,Sn=n2,从而Sk2=(Sk)2成立,
综上所述,只有3个满足条件的无穷等差数列,分别为an=0或an=1或an=2n-1.
故答案为:(1)4;(2)an=0或an=1或an=2n-1
点评:本题考查等差数列的性质,等差数列的前n项和公式,以及等差数列的通项公式,解题时要认真审题,仔细解答,注意合理地进行等价转化,熟练掌握性质及公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,公差d=1.求满足
,公差d=1.求满足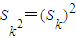 的正整数k;
的正整数k;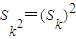 成立.
成立.