��Ŀ����
����Ŀ�����ڣ�ij������˾�ֱ��Ƴ�֧��������ɨ��֧���˳�����������һ��ʱ����ƹ��ڣ������ƹ������Ż����Ƚϴ�����Խ��Խ����˿�ʼʹ��ɨ��֧��.ij��·��������ͳ���˻���Ƴ�һ����ÿһ��ʹ��ɨ��֧�����˴Σ���![]() ��ʾ��Ƴ���������
��ʾ��Ƴ���������![]() ��ʾÿ��ʹ��ɨ��֧�����˴Σ���λ��ʮ�˴Σ���ͳ���������1��ʾ��
��ʾÿ��ʹ��ɨ��֧�����˴Σ���λ��ʮ�˴Σ���ͳ���������1��ʾ��
��һ
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
�����������ݣ�����������ͼ��ʾ��ɢ��ͼ.
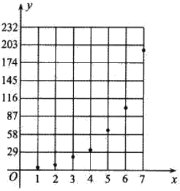
��1������ɢ��ͼ�жϣ����ƹ����ڣ�![]() ��
��![]() ��
��![]() ��
��![]() ��Ϊ������ij�������һ��������Ϊɨ��֧�����˴�
��Ϊ������ij�������һ��������Ϊɨ��֧�����˴�![]() ���ڻ�Ƴ�����
���ڻ�Ƴ�����![]() �Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ���
�Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ���
��2�����ݣ�1�����жϽ������1�е����ݣ���![]() ����
����![]() �Ļع鷽�̣���Ԥ���Ƴ���8��ʹ��ɨ��֧�����˴Σ�
�Ļع鷽�̣���Ԥ���Ƴ���8��ʹ��ɨ��֧�����˴Σ�
��3���ƹ��ڽ������ӶԳ˿͵�֧����ʽ����ͳ�ƣ�������2
��2
֧����ʽ | �ֽ� | �˳��� | ɨ�� |
���� | 10% | 60% | 30% |
��֪����·������Ʊ��Ϊ2Ԫ��ʹ���ֽ�֧���ij˿����Żݣ�ʹ�ó˳���֧���ij˿�����8���Żݣ�ɨ��֧���ij˿�����Żݣ�����ͳ�ƽ����֪��ʹ��ɨ��֧���ij˿ͣ�����7���Żݵĸ���Ϊ![]() ������8���Żݵĸ���Ϊ
������8���Żݵĸ���Ϊ![]() ������9���Żݵĸ���Ϊ
������9���Żݵĸ���Ϊ![]() �����������������¼�������Ƶ����Ϊ��Ӧ�¼������ĸ��ʣ�����һ���˿�һ�γ˳���ƽ������.
�����������������¼�������Ƶ����Ϊ��Ӧ�¼������ĸ��ʣ�����һ���˿�һ�γ˳���ƽ������.
�ο����ݣ�
|
|
|
|
|
62.14 | 1.54 | 2535 | 50.12 | 3.47 |
����![]() ��
��![]()
�ο���ʽ������һ������![]() ��
��![]() ������
������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��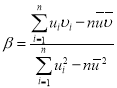 ��
��![]() .
.
���𰸡�(1) ![]() ���� (2)
���� (2) ![]() ��3470��(3)1.66Ԫ
��3470��(3)1.66Ԫ
��������
��1������ɢ��ͼ�����ж�![]() ��ϽϺã�2������ȡ����ת��Ϊ���Իع鷽������
��ϽϺã�2������ȡ����ת��Ϊ���Իع鷽������![]() ���������ݼ������
���������ݼ������![]() ����ת��Ϊ
����ת��Ϊ![]() ������
������![]() Ԥ�⼴�ɣ�3����һ���˿ͳ˳�֧���ķ���Ϊ
Ԥ�⼴�ɣ�3����һ���˿ͳ˳�֧���ķ���Ϊ![]() ��д��
��д��![]() �Ŀ���ȡֵ������������ʣ����ݷֲ���������������.
�Ŀ���ȡֵ������������ʣ����ݷֲ���������������.
��1������ɢ��ͼ�жϣ�![]() ������Ϊɨ��֧��������
������Ϊɨ��֧��������![]() ���ڻ�Ƴ�����
���ڻ�Ƴ�����![]() �Ļع鷽�����ͣ�
�Ļع鷽�����ͣ�
��2����![]() ������ͬʱȡ���ö����ã�
������ͬʱȡ���ö����ã�![]() ��
��
��![]() ����
����![]()
��![]() ��
��![]() ��
��![]() ��
��
��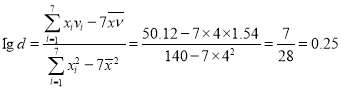 ��
��
���������ĵ�![]() ����
����![]() ���ã�
���ã�![]() ��
��
��![]() ����
����![]() ��
��
��![]() ����
����![]() �Ļع鷽��ʽ��
�Ļع鷽��ʽ��![]() ��
��
��![]() ������ʽ��
������ʽ��![]() ��
��
��Ƴ���8��ʹ��ɨ��֧�����˴�Ϊ3470��
��3����һ���˿ͳ˳�֧���ķ���Ϊ![]() ����
����![]() ��ȡֵ����Ϊ��2��1.8��1.6��1.4��
��ȡֵ����Ϊ��2��1.8��1.6��1.4��
![]() ��
��![]() ��
��
![]() ��
��![]() .
.
�ֲ���Ϊ��
| 2 | 1.8 | 1.6 | 1.4 |
| 0.1 | 0.15 | 0.7 | 0.05 |
���ԣ�һ���˿�һ�γ˳���ƽ������Ϊ��
![]() ��Ԫ��
��Ԫ��

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�