题目内容
【题目】某公园草坪上有一扇形小径(如图),扇形半径为![]() ,中心角为
,中心角为![]() ,甲由扇形中心
,甲由扇形中心![]() 出发沿
出发沿![]() 以每秒2米的速度向
以每秒2米的速度向![]() 快走,同时乙从
快走,同时乙从![]() 出发,沿扇形弧以每秒
出发,沿扇形弧以每秒![]() 米的速度向
米的速度向![]() 慢跑,记
慢跑,记![]() 秒时甲、乙两人所在位置分别为
秒时甲、乙两人所在位置分别为![]() ,
,![]() ,通过计算
,通过计算![]() ,判断下列说法是否正确:
,判断下列说法是否正确:

(1)当![]() 时,函数
时,函数![]() 取最小值;
取最小值;
(2)函数![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(3)若![]() 最小,则
最小,则![]() ;
;
(4)![]() 在
在![]() 上至少有两个零点;
上至少有两个零点;
其中正确的判断序号是______(把你认为正确的判断序号都填上)
【答案】②③④
【解析】
建立如下图所示的平面直角坐标系,根据题意求出![]() 两点坐标,求出
两点坐标,求出![]() ,并计算出
,并计算出![]() 的值,对四个选项逐一判断即可.
的值,对四个选项逐一判断即可.
建立如下图所示的平面直角坐标系,

因为甲由扇形中心![]() 出发沿
出发沿![]() 以每秒2米的速度向
以每秒2米的速度向![]() 快走,所以
快走,所以![]() ,
,
乙从![]() 出发,沿扇形弧以每秒
出发,沿扇形弧以每秒![]() 米的速度向
米的速度向![]() 慢跑,所以
慢跑,所以 ,因此
,因此![]() ,其中
,其中![]()

![]() ,
,
![]()
当![]() 时
时![]() ,因为
,因为![]() ,所以此时函数
,所以此时函数![]() 不是最小值;
不是最小值;
当![]() 时
时![]() ,当
,当![]() 时,结合图象可得M向左上方移动,而N沿x正半轴向右边移动,因此MN越来越大,
时,结合图象可得M向左上方移动,而N沿x正半轴向右边移动,因此MN越来越大,![]() 增函数
增函数
由于当![]() 时,
时,![]() ,而
,而![]() 所以若
所以若![]() 最小,则
最小,则![]() ;
;
由![]() 得
得![]() ,因为
,因为![]() ,
,![]() 所以
所以![]() 时,存在
时,存在![]() ,即
,即![]() 在
在![]() 上至少有两个零点;
上至少有两个零点;
故答案为:②③④

【题目】某家具公司生产甲、乙两种书柜,制柜需先制白胚再油漆,每种柜的制造白胚工时数、油漆工时数的有关数据如下:
工艺要求 | 产品甲 | 产品乙 | 生产能力(工时/天) |
制白胚工时数 | 6 | 12 | 120 |
油漆工时数 | 8 | 4 | 64 |
单位利润 | 20元 | 24元 |
则该公司合理安排这两种产品的生产,每天可获得的最大利润为______.
【题目】在贯彻中共中央、国务院关于精准扶贫政策的过程中,某单位在某市定点帮扶甲、乙两村各![]() 户贫困户.为了做到精准帮扶,工作组对这
户贫困户.为了做到精准帮扶,工作组对这![]() 户村民的年收入情况、劳动能力情况.子女受教育情况、危旧房情况、患病情况等进行调查.并把调查结果转化为各户的贫困指标
户村民的年收入情况、劳动能力情况.子女受教育情况、危旧房情况、患病情况等进行调查.并把调查结果转化为各户的贫困指标![]() .将指标
.将指标![]() 按照
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
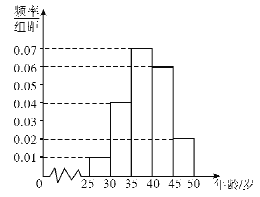
,![]() 分成五组,得到如图所示的频率分布直方图.规定若
分成五组,得到如图所示的频率分布直方图.规定若![]() ,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”,且当
,则认定该户为“绝对贫困户”,否则认定该户为“相对贫困户”,且当![]() 时,认定该户为“低收入户”;当
时,认定该户为“低收入户”;当![]() 时,认定该户为“亟待帮助户".已知此次调查中甲村的“绝对贫困户”占甲村贫困户的
时,认定该户为“亟待帮助户".已知此次调查中甲村的“绝对贫困户”占甲村贫困户的![]() .
.
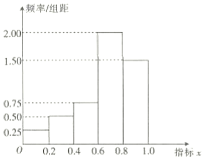
(1)完成下面的列联表,并判断是否有![]() 的把握认为绝对贫困户数与村落有关:
的把握认为绝对贫困户数与村落有关:
甲村 | 乙村 | 总计 | |
绝对贫困户 | |||
相对贫困户 | |||
总计 |
(2)某干部决定在这两村贫困指标处于![]() 的贫困户中,随机选取
的贫困户中,随机选取![]() 户进行帮扶,用
户进行帮扶,用![]() 表示所选
表示所选![]() 户中“亟待帮助户”的户数,求
户中“亟待帮助户”的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
【题目】近期,某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表一
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据,绘制了如下图所示的散点图.

(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() ,
,![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表1中的数据,求![]() 关于
关于![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次;
的回归方程,并预测活动推出第8天使用扫码支付的人次;
(3)推广期结束后,车队对乘客的支付方式进行统计,结果如表2
表2
支付方式 | 现金 | 乘车卡 | 扫码 |
比例 | 10% | 60% | 30% |
已知该线路公交车票价为2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客,享受7折优惠的概率为![]() ,享受8折优惠的概率为
,享受8折优惠的概率为![]() ,享受9折优惠的概率为
,享受9折优惠的概率为![]() .根据所给数据以事件发生的频率作为相应事件发生的概率,估计一名乘客一次乘车的平均费用.
.根据所给数据以事件发生的频率作为相应事件发生的概率,估计一名乘客一次乘车的平均费用.
参考数据:
|
|
|
|
|
62.14 | 1.54 | 2535 | 50.12 | 3.47 |
其中![]() ,
,![]()
参考公式:对于一组数据![]() ,
,![]() ,……
,……![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.