题目内容
已知ω>0,函数f(x)=sin 在
在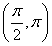 上单调递减,则ω的取值范围是________.
上单调递减,则ω的取值范围是________.
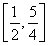
【解析】由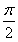 +2kπ≤
+2kπ≤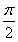 ω+
ω+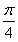 <πω+
<πω+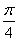 ≤
≤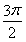 +2kπ,k∈Z,得
+2kπ,k∈Z,得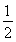 +4k≤ω≤
+4k≤ω≤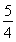 +2k,k∈Z.∵ω>0,∴
+2k,k∈Z.∵ω>0,∴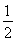 ≤ω≤
≤ω≤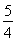 .
.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
题目内容
已知ω>0,函数f(x)=sin 在
在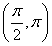 上单调递减,则ω的取值范围是________.
上单调递减,则ω的取值范围是________.
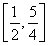
【解析】由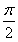 +2kπ≤
+2kπ≤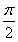 ω+
ω+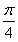 <πω+
<πω+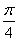 ≤
≤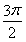 +2kπ,k∈Z,得
+2kπ,k∈Z,得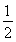 +4k≤ω≤
+4k≤ω≤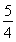 +2k,k∈Z.∵ω>0,∴
+2k,k∈Z.∵ω>0,∴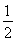 ≤ω≤
≤ω≤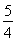 .
.

 优百分课时互动系列答案
优百分课时互动系列答案