题目内容
已知函数f(x)=sinx-
cosx+2，记函数f（x）的最小正周期为β，向量
=(2，cosα)，
=(1，tan(α+
))（0＜α＜
），且
•
=
．
（Ⅰ）求f（x）在区间[
，
]上的最值；
（Ⅱ）求
的值．
| 3 |
| a |
| b |
| β |
| 2 |
| π |
| 4 |
| a |
| b |
| 7 |
| 3 |
（Ⅰ）求f（x）在区间[
| 2π |
| 3 |
| 4π |
| 3 |
（Ⅱ）求
| 2cos2α-sin2(α+β) |
| cosα-sinα |
（Ⅰ）根据题意，可得
f(x)=sinx-
cosx+2=2(sinxcos
-cosxsin
)+2=2sin(x-
)+2．
∵x∈[
，
]，可得x-
∈[
，π]，∴sin(x-
)∈[0，
]，
当x=
时，f（x）的最小值是2；当x=
时，f（x）的最大值是4．
（Ⅱ）∵f（x）=2sin(x-
)+2的周期T=2π，∴β=2π，
由此可得
•
=2+cosα•tan(α+
)=2+cosαtan(α+π)=2+sinα=
，解之得sinα=
．
∴
=
=
=
=2cosα，
∵0＜α＜
，可得cosα=
=
，
∴
=2cosα=
．
f(x)=sinx-
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∵x∈[
| 2π |
| 3 |
| 4π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
当x=
| 4π |
| 3 |
| 5π |
| 6 |
（Ⅱ）∵f（x）=2sin(x-
| π |
| 3 |
由此可得
| a |
| b |
| β |
| 2 |
| 7 |
| 3 |
| 1 |
| 3 |
∴
| 2cos2α-sin2(α+β) |
| cosα-sinα |
| 2cos2α-sin2(α+π) |
| cosα-sinα |
| 2cos2α-sin2α |
| cosα-sinα |
| 2cosα(cosα-sinα) |
| cosα-sinα |
∵0＜α＜
| π |
| 4 |
| 1-sin2α |
2
| ||
| 3 |
∴
| 2cos2α-sin2(α+β) |
| cosα-sinα |
4
| ||
| 3 |
练习册系列答案
相关题目
.
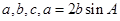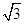，c＝5，求b.
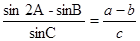，则角A的大小为（ ）.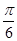
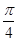
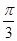
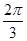
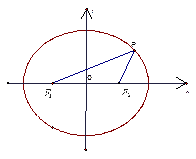
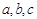分别为
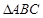的三个内角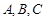
的对边，
，
，
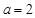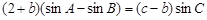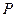是以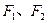
为焦点的椭圆上一点，且
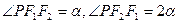，求证：椭圆的离心率为
.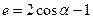