题目内容
若α∈(0,π),且3cos2α=sin(
-α),则sin2α的值为( )
| π |
| 4 |
A.1或-
| B.1 | C.
| D.-
|
由于α∈(0,π),且3cos2α=sin(
-α),
则3(cos2α-sin2α)=
(cosα-sinα),
即3(cosα-sinα)(cosα+sinα)=
(cosα-sinα),
∴cosα-sinα=0 ①,或 cosα+sinα=
②.
由①可得,α=
,sin2α=sin
=1.
由②可得 (cosα+sinα)2=1+2sinαcosα=
,
∴sin2α=2sinαcosα=-
.
综上可得,sin2α的值为 1或-
.
故选A.
| π |
| 4 |
则3(cos2α-sin2α)=
| ||
| 2 |
即3(cosα-sinα)(cosα+sinα)=
| ||
| 2 |
∴cosα-sinα=0 ①,或 cosα+sinα=
| ||
| 6 |
由①可得,α=
| π |
| 4 |
| π |
| 2 |
由②可得 (cosα+sinα)2=1+2sinαcosα=
| 1 |
| 18 |
∴sin2α=2sinαcosα=-
| 17 |
| 18 |
综上可得,sin2α的值为 1或-
| 17 |
| 18 |
故选A.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
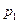 :
: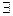 x
x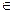 R,
R, 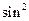
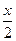 +
+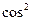
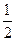
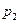 :
:  :
: 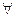 x
x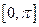 ,
,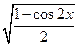 ="sinx "
="sinx " 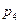 : sinx=cosy
: sinx=cosy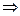 x+y=
x+y=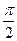
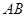 的中点,点D,E分别在半径OA,OB上.若
的中点,点D,E分别在半径OA,OB上.若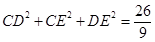 ,则
,则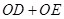 的最大值是 .
的最大值是 .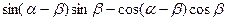 =m,且α是第三象限角,则sinα=
=m,且α是第三象限角,则sinα=