题目内容
3．设集合P={x|y=log2x}，Q=|y|y=x3}，则P∩Q等于（ ）| A． | R | B． | [0，+∞） | C． | （0，+∞） | D． | [1，+∞） |
分析 求出集合的等价条件，根据集合的基本运算进行求解即可．
解答 解：P={x|y=log2x}=（0，+∞），
Q=|y|y=x3}=（-∞，+∞），
则P∩Q=（0，+∞），
故选：C
点评 本题主要考查集合的基本运算，比较基础．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
14．
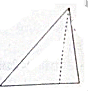已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成，其正视图为如图所示的直角三角形（其中虚线长度为$\sqrt{5}$），则此四棱锥的体积是（ ）
已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成，其正视图为如图所示的直角三角形（其中虚线长度为$\sqrt{5}$），则此四棱锥的体积是（ ）| A． | 14 | B． | 7$\sqrt{5}$ | C． | $\frac{14}{3}$ | D． | $\frac{2\sqrt{5}}{3}$ |
11．若函数f（x）=$\frac{x}{\sqrt{1+{x}^{2}}}$，f（2）（x）=f[f（x）]，f（3）（x）=f（f（f（x））），则f（99）（1）=$\frac{1}{10}$．
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$，x∈R）的图象的一部分如图所示．
13．用数学归纳法证明：“两两相交且不共点的n条直线把平面分为f（n）部分，则f（n）=1+$\frac{n（n+1）}{2}$．”在证明第二步归纳递推的过程中，用到f（k+1）=f（k）+（ ）
| A． | k-1 | B． | k | C． | k+1 | D． | $\frac{k（k+1）}{2}$ |