题目内容
4.设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x+2.(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成图形的面积;
(3)若直线x=-t(0<t<1把y=f(x)的图象与两坐标轴所围成图形的面积二等分,求t的值.
分析 (1)利用待定系数即可求y=f(x)的表达式;
(2)求函数的积分,根据积分即可y=f(x)的图象与两坐标轴所围成图形的面积;
(3)由${∫}_{-1}^{-t}$ ( x2+2x+1)dx=${∫}_{-t}^{0}$( x2+2x+1)dx,解方程即可.
解答 解:(1)设f(x)=ax2+bx+c,则f′(x)=2ax+b,
又已知f′(x)=2x+2,
∴a=1,b=2.∴f(x)=x2+2x+c
又方程f(x)=0有两个相等实根,
∴判别式△=4-4c=0,即c=1.故f(x)=x2+2x+1.
(2)依题意f(x)=x2+2x+1=(x+1)2,
∴所求面积S=${∫}_{-1}^{0}$(x2+2x+1)dx=($\frac{1}{3}{x}^{3}+{x}^{2}+x$)|${\;}_{-1}^{0}$=$\frac{1}{3}$.
(3)由题意可得${∫}_{-1}^{-t}$ ( x2+2x+1)dx=${∫}_{-t}^{0}$( x2+2x+1)dx,
即 ($\frac{1}{3}$x3+x2+x)${|}_{-1}^{-t}$=($\frac{1}{3}$x3+x2+x)${|}_{-t}^{0}$,
即-$\frac{1}{3}$ t3+t2-t+$\frac{1}{3}$=$\frac{1}{3}$ t3-t2+t,
∴2t3-6t2+6t-1=0,
即2(t-1)3=-1,∴t=1-$\frac{1}{\root{3}{2}}$.
点评 本题主要考查用待定系数法求函数的解析式,导数的运算,定积分的应用,属于中档题.

练习册系列答案
相关题目
8.在等比数列{an}中,若a4=1,a7=8,则公比q=( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | 2 |
15.610°是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
19.定义运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,若函数f(x)=$|\begin{array}{l}{x-1}&{2}\\{-x}&{x+3}\end{array}|$在(-∞,m)上单调递减,则实数m的取值范围( )
| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-∞,-2) | D. | (-∞,-2] |
14.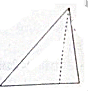 已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )
已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )
 已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )
已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )| A. | 14 | B. | 7$\sqrt{5}$ | C. | $\frac{14}{3}$ | D. | $\frac{2\sqrt{5}}{3}$ |