题目内容
4.已知函数y=tanωx(ω>0)在(-$\frac{π}{6}$,$\frac{π}{4}$)上单调递增,则ω的最大值为2.分析 根据正切函数的单调性和单调区间进行求解即可.
解答 解:函数数y=tanωx(ω>0)的周期T=$\frac{π}{ω}$,
∵|-$\frac{π}{6}$|<$\frac{π}{4}$,
∴由正切函数的单调性可得$\frac{T}{2}$$≥\frac{π}{4}$,即可,
即T=$\frac{π}{ω}$≥$\frac{π}{2}$,
即0<ω≤2,
故ω的最大值为2,
故答案为:2
点评 本题主要考查三角函数单调性的应用,根据条件确定T=$\frac{π}{ω}$≥$\frac{π}{2}$是解决本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
14.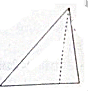 已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )
已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )
 已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )
已知一个四棱锥的底面由不等式组$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x+y≤2}\\{y-x-4≤0}\end{array}\right.$确定的平面区域构成,其正视图为如图所示的直角三角形(其中虚线长度为$\sqrt{5}$),则此四棱锥的体积是( )| A. | 14 | B. | 7$\sqrt{5}$ | C. | $\frac{14}{3}$ | D. | $\frac{2\sqrt{5}}{3}$ |
13.用数学归纳法证明:“两两相交且不共点的n条直线把平面分为f(n)部分,则f(n)=1+$\frac{n(n+1)}{2}$.”在证明第二步归纳递推的过程中,用到f(k+1)=f(k)+( )
| A. | k-1 | B. | k | C. | k+1 | D. | $\frac{k(k+1)}{2}$ |
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.