题目内容
函数f(x)=Asin(wx+j)(A>0,w>0,- <j<
<j< ,x∈R)的部分图象如图所示:
,x∈R)的部分图象如图所示: ,
,
(1)求函数y=f(x)的解析式;(2)当x∈ 时,求f(x)的取值范围.
时,求f(x)的取值范围.
 <j<
<j< ,x∈R)的部分图象如图所示:
,x∈R)的部分图象如图所示: ,
,(1)求函数y=f(x)的解析式;(2)当x∈
 时,求f(x)的取值范围.
时,求f(x)的取值范围.(1)f(x)=sin(x+ );(2)[-1,
);(2)[-1,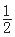 ].
].
 );(2)[-1,
);(2)[-1,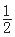 ].
].试题分析:(1)图像离平衡位置最高值为1可知A=1,又从图可看出周期的四分之一为
 ,根据
,根据 可求得w的值,对于j可通过代入(
可求得w的值,对于j可通过代入(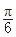 ,1)点求得,但要注意j的范围;(2)本小题考查三角函数求值域问题,由x的范围可先求出x+
,1)点求得,但要注意j的范围;(2)本小题考查三角函数求值域问题,由x的范围可先求出x+ 的范围,结合正弦函数图像可求出sin(x+
的范围,结合正弦函数图像可求出sin(x+ )的取值范围.
)的取值范围.试题解析:(1)由图象得A=1,
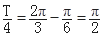 ,所以T=2p,则w="1." 将点(
,所以T=2p,则w="1." 将点(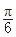 ,1)代入得sin(
,1)代入得sin(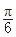 +j)=1,而-
+j)=1,而- <j<
<j< ,所以j=
,所以j= ,因此函数f(x)=sin(x+
,因此函数f(x)=sin(x+ ).
).(2)由于x∈
 ,-
,-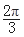 ≤x+
≤x+ ≤
≤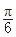 ,所以-1≤sin(x+
,所以-1≤sin(x+ )≤
)≤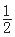 ,所以f(x)的取值范围[-1,
,所以f(x)的取值范围[-1,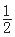 ].
]. ,三角函数的值域问题.
,三角函数的值域问题.
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
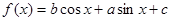 .
.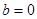 时,求
时,求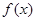 的值域;
的值域;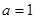 ,
,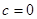 时,函数
时,函数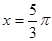 对称,求函数
对称,求函数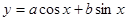 的对称轴;
的对称轴;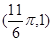 ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的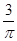 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得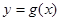 的图象,又知
的图象,又知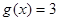 的所有正根从小到大依次为
的所有正根从小到大依次为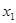 ,
,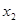 ,…
,…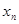 ,…且
,…且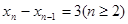 ,求
,求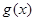 的解析式.
的解析式.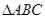 中,角
中,角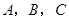 所对的边分别为
所对的边分别为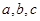 ,且
,且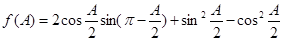
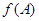 的最大值;
的最大值;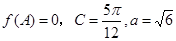 ,求
,求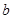 的值.
的值.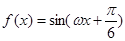 (ω>0),把函数
(ω>0),把函数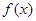 的图象向右平移
的图象向右平移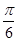 个单位长度,所得图象的一条对称轴方程是x=
个单位长度,所得图象的一条对称轴方程是x=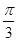 ,则ω的最小值是 .
,则ω的最小值是 .  (
( )的图象如图所示,则
)的图象如图所示,则 值为( )
值为( )




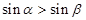 ,那么下列命题成立的是( )
,那么下列命题成立的是( )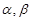 是第一象限角,则
是第一象限角,则

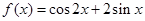 的最小值和最大值分别为( )
的最小值和最大值分别为( )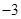 、
、
 、
、
 、
、
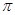 的周期函数,且当
的周期函数,且当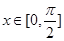 时,
时,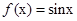 ,则
,则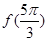 的值是 .
的值是 .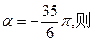
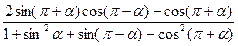 的值等于( )
的值等于( )
