题目内容
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,若
,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)在(1)的条件下,设![]() 为整数,且对于任意正整数
为整数,且对于任意正整数![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)1;(2)2
【解析】试题分析:(1)求出函数的导数,求出h(x)的解析式,求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的最小值,求出a的值即可;(2)得到1+x≤ex,令x=﹣![]() (n∈N*,k=0,1,2,3,…,n﹣1),则0<1﹣
(n∈N*,k=0,1,2,3,…,n﹣1),则0<1﹣![]() ≤
≤![]() ,得到
,得到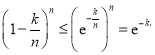 累加,通过放大不等式,证明即可.
累加,通过放大不等式,证明即可.
解析:
(1)因为![]() ,所以
,所以![]() ,
,
由![]() 对任意的
对任意的![]() 恒成立,即
恒成立,即![]() ,由
,由![]() ,
,
(i)当![]() 时,
时, ![]() ,
, ![]() 的单调递增区间为
的单调递增区间为![]() ,
,
所以![]() 时,
时, ![]() ,所以不满足题意.
,所以不满足题意.
(ii)当![]() 时,由
时,由![]() ,得
,得![]()
![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
所以![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以![]() 的最小值为
的最小值为![]() .
.
设![]() ,所以
,所以![]() ,① 因为
,① 因为![]() ,令
,令![]() 得
得![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
所以![]() ,②,由①②得
,②,由①②得![]() ,则
,则![]() .
.
(2)由(1)知![]() ,即
,即![]() ,
,
令![]() (
(![]() ,
, ![]() )则
)则![]() ,
,
所以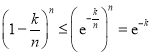 ,
,
所以![]()
![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() 的最小值为
的最小值为![]()

练习册系列答案
相关题目