题目内容
【题目】已知抛物线![]() 的焦点为F,直线
的焦点为F,直线![]() 与x轴的交点为P,与抛物线的交点为Q,且
与x轴的交点为P,与抛物线的交点为Q,且![]() .
.
(1)求抛物线的方程;
(2)过F的直线l与抛物线相交于A,D两点,与圆![]() 相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
【答案】(1)x2=4y;(2)1.
【解析】试题分析:(1)利用![]() 构建关于
构建关于![]() 的方程,解得
的方程,解得![]() ,也就是抛物线的方程为
,也就是抛物线的方程为![]() .(2)设直线
.(2)设直线![]() ,利用焦半径公式可以得到
,利用焦半径公式可以得到![]() ,其中
,其中![]() 为
为![]() 到直线
到直线![]() 的距离,联立直线和抛物线的方程,消去
的距离,联立直线和抛物线的方程,消去![]() 后可以得到
后可以得到![]() ,利用导数可以求出过
,利用导数可以求出过![]() 的切线方程,从而求出
的切线方程,从而求出![]() ,故
,故![]() ,从而求出面积乘积的最小值为
,从而求出面积乘积的最小值为![]() .
.
解析:(1)由题意可知![]() ,由
,由 ![]() ,则
,则![]() ,解得
,解得![]() ,∴抛物线
,∴抛物线![]() .
.
(2)设![]() ,联立
,联立 ![]() ,整理得:
,整理得: ![]() , 则
, 则![]() ,由
,由![]() ,求导
,求导![]() ,直线
,直线![]() 同理求得
同理求得![]() ,则
,则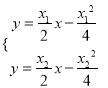 ,解得:
,解得: ![]() ,则
,则![]() ,
, ![]() 到
到![]() 的距离
的距离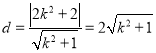 ,
, ![]() 与
与![]() 的面积之积为:
的面积之积为:
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目