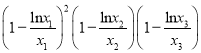题目内容
【题目】某校为了鼓励学生热心公益,服务社会,成立了“慈善义工社”.2017年12月,该校“慈善义工社”为学生提供了4次参加公益活动的机会,学生可通过网路平台报名参加活动.为了解学生实际参加这4次活动的情况,该校随机抽取100名学生进行调查,数据统计如下表,其中“√”表示参加,“×”表示未参加.
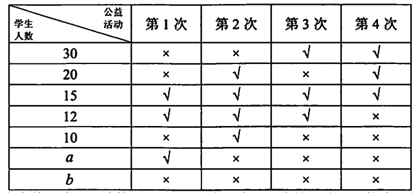
根据表中数据估计,该校4000名学生中约有120名这4次活动均未参加.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从该校4000名学生中任取一人,试估计其2017年12月恰参加了2次学校组织的公益活动的概率;
(Ⅲ)已知学生每次参加公益活动可获得10个公益积分,任取该校一名学生,记该生2017年12月获得的公益积分为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【答案】(Ⅰ)![]() ,
, ![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)21.6
(Ⅲ)21.6
【解析】试题分析:(Ⅰ)依题意![]() ,及学生人数和为100,即可求解
,及学生人数和为100,即可求解![]() 的值;
的值;
(Ⅱ)将表格中参加了2次学校组织的公益活动的频率作为概率估计即可;
(Ⅲ)![]() 可取0,10,20,30,40,分别计算概率得分布列,利用期望公式求解期望即可.
可取0,10,20,30,40,分别计算概率得分布列,利用期望公式求解期望即可.
试题解析:
(Ⅰ)依题意![]() ,所以
,所以![]() .
.
因为![]() ,
,
所以![]() ,
, ![]() .
.
(Ⅱ)设“从该校所有学生中任取一人,其2017年12月恰参加了2次学校组织的公益活动”为事件![]() ,
,
则![]() .
.
所以从该校所有学生中任取一人,其2017年12月恰参加了2次学校组织的公益活动的概率约为![]() .
.
(Ⅲ)![]() 可取0,10,20,30,40.
可取0,10,20,30,40.
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
所以随机变量![]() 的分布列为:
的分布列为:

所以![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目