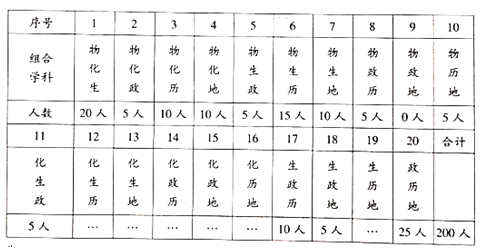
题目内容
【题目】已知数列![]() ,
,![]() ,且
,且![]() 对任意n
对任意n![]() 恒成立.
恒成立.
(1)求证:![]() (n
(n![]() );
);
(2)求证:![]() (n
(n![]() ).
).
【答案】(1)见解析(2)见解析
【解析】
(1)利用数学归纳法直接证明,假设当![]() 时,
时,![]() 成立,则当
成立,则当![]() 时,
时,![]() ,将
,将![]() 代入即可证得:当
代入即可证得:当![]() 时,
时,![]() 成立,问题得证。
成立,问题得证。
(2)利用数学归纳法证明,先证明![]() 时,
时,![]() 成立,假设当
成立,假设当![]() 时,
时, ![]() 成立,证明:当
成立,证明:当![]() 时,
时,![]() 成立,
成立,
因为![]() ,可将证明
,可将证明![]() 问题转化成:证明
问题转化成:证明![]() ,转化成证明
,转化成证明![]() ,再转化成证明
,再转化成证明![]() (
(![]() )成立。构造函数
)成立。构造函数![]() ,利用导数即可判函数
,利用导数即可判函数![]() 在
在![]() 上递增,结合
上递增,结合![]() ,即可证得:当
,即可证得:当![]() 时,
时,![]() 成立,即可证得:当
成立,即可证得:当![]() ,
,![]() 成立,问题得证。
成立,问题得证。
(1)①当![]() 时,
时,![]()
满足![]() 成立.
成立.
②假设当![]() 时,结论成立.即:
时,结论成立.即:![]() 成立
成立
下证:当![]() 时,
时,![]() 成立。
成立。
因为![]()
![]()
即:当![]() 时,
时,![]() 成立
成立
由①、②可知,![]() (n
(n![]() )成立。
)成立。
(2)(ⅰ)当![]() 时,
时,![]() 成立,
成立,
当![]() 时,
时,![]() 成立,
成立,
(ⅱ)假设![]() 时(
时(![]() ),结论正确,即:
),结论正确,即:![]() 成立
成立
下证:当![]() 时,
时,![]() 成立.
成立.
因为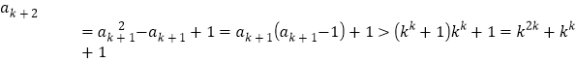
要证![]() ,
,
只需证![]()
只需证:![]() ,
,
只需证:![]()
即证:![]() (
(![]() )
)
记![]()
![]()
![]()
![]()
当![]() 时,
时,![]()
所以![]() 在
在![]() 上递增,
上递增,
又![]()
所以,当![]() 时,
时,![]() 恒成立。
恒成立。
即:当![]() 时,
时,![]() 成立。
成立。
即:当![]() 时,
时,![]() 恒成立.
恒成立.
所以当![]() ,
,![]() 恒成立.
恒成立.
由(ⅰ)(ⅱ)可得:对任意的正整数![]() ,不等式
,不等式![]() 恒成立,命题得证.
恒成立,命题得证.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案【题目】南方智运汽车公司在我市推出了共享汽车“Warmcar”,有一款车型为“众泰云”新能源共享汽车,其中一种租用方式“分时计费”规则为:0.15元/分钟+0.8元/公里.已知小李家离上班地点为10公里,每天租用该款汽车上、下班各一次,由于堵车、及红绿灯等原因每次路上开车花费的时间![]() (分钟)是一个随机变量,现统计了100次路上开车花费时间,在各时间段内是频数分布情况如下表所示:
(分钟)是一个随机变量,现统计了100次路上开车花费时间,在各时间段内是频数分布情况如下表所示:
时间 |
|
|
|
|
|
|
|
频数 | 2 | 6 | 14 | 36 | 28 | 10 | 4 |
(1)写出小李上班一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分钟)的函数关系;
(分钟)的函数关系;
(2)根据上面表格估计小李平均每次租车费用;
(3)“众泰云”新能源汽车还有一种租用方式为“按月计费”,规则为每个月收取租金2350元,若小李每个月上班时间平均按21天计算,在不计电费和情况下,请你为小李选择一种省钱的租车方式.
【题目】近年来,某地区积极践行“绿水青山就是金山银山”的绿色发展理念![]() 年年初至
年年初至![]() 年年初,该地区绿化面积
年年初,该地区绿化面积![]() (单位:平方公里)的数据如下表:
(单位:平方公里)的数据如下表:
年份 |
|
|
|
|
|
|
|
年份代号 |
|
|
|
|
|
|
|
绿化面积 |
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测该地区![]() 年年初的绿化面积,并计算
年年初的绿化面积,并计算![]() 年年初至
年年初至![]() 年年初,该地区绿化面积的年平均增长率约为多少.
年年初,该地区绿化面积的年平均增长率约为多少.
(附:回归直线的斜率与截距的最小二乘法估计公式分别为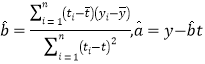 ,
,![]() )
)