题目内容
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 是菱形,
是菱形,![]() ⊥平面
⊥平面![]() 且
且![]() .
.
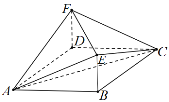
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)若![]() 设
设![]() 与平面
与平面![]() 所成夹角为
所成夹角为![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
分析:(1)根据已知可得![]() 和
和![]() ,由线面垂直判定定理可证
,由线面垂直判定定理可证![]() 平面
平面![]() ,再由面面垂直判定定理证得平面
,再由面面垂直判定定理证得平面![]() ⊥平面
⊥平面![]() .
.
(2)解法一:向量法,设![]() ,以
,以![]() 为原点,作
为原点,作![]() ,以
,以![]() 的方向分别为
的方向分别为![]() 轴,
轴,![]() 轴的正方向,建空间直角坐标系,求得
轴的正方向,建空间直角坐标系,求得![]() 的坐标,运用向量的坐标表示和向量的垂直条件,求得平面
的坐标,运用向量的坐标表示和向量的垂直条件,求得平面![]() 和平面
和平面![]() 的的法向量,再由向量的夹角公式,计算即可得到所求的值.
的的法向量,再由向量的夹角公式,计算即可得到所求的值.
解法二:三垂线法,连接AC交BD于O,连接EO、FO,过点F做FM⊥EC于M,连OM,由已知可以证明FO⊥面AEC,∠FMO即为二面角A-EC-F的平面角,通过菱形的性质、勾股定理和等面积法求得cos∠FMO,得到答案.
解法三:射影面积法,连接AC交BD于O,连接EO、FO,根据已知条件计算![]() ,
,![]() ,二面角的余弦值cosθ=
,二面角的余弦值cosθ=![]() ,即可求得答案.
,即可求得答案.
详解:(1)证明:连结![]()
![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,
![]() ⊥平面
⊥平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ⊥平面
⊥平面![]() .
.
(2)解:解法一:设 ![]() ,
,
![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,
![]() 、
、![]() 为等边三角形,
为等边三角形,![]()
![]() ,
,
![]()
![]() 是
是![]() 的中点,
的中点, ![]()
![]() ,
,
![]()
![]() ⊥平面
⊥平面![]() ,
,![]() ,
,
![]() 在
在![]() 中有,
中有,![]() ,
,![]() ,
,
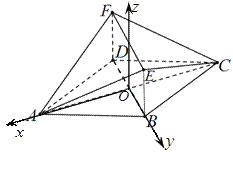
以![]() 为原点,作
为原点,作![]() ,以
,以![]() 的方向分别为
的方向分别为![]() 轴,
轴,![]() 轴的正方向,建空间直角坐标系
轴的正方向,建空间直角坐标系![]() 如图所示,则
如图所示,则![]()
所以![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
由 得
得![]() 设
设![]() ,解得
,解得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由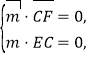 得
得![]() 设
设![]() ,解得
,解得![]() .
.
设二面角![]() 的为
的为![]() ,则
,则![]()
结合图可知,二面角![]() 的余弦值为
的余弦值为![]() .
.
解法二:
∵EB⊥面ABCD,
∴∠EAB即为EA与平面ABCD所成的角
在Rt△EAB中,cos∠EAB=![]() 又AB=2,∴AE=
又AB=2,∴AE=![]()
∴EB=DF=1
连接AC交BD于O,连接EO、FO
菱形ABCD中,∠BAD=60°,∴BD=AB=2
矩形BEFD中,FO=EO=![]() ,EF=2,EO+FO=EF,∴FO⊥EO
,EF=2,EO+FO=EF,∴FO⊥EO
又AC⊥面BEFD, FO面BEFD,∴FO⊥AC,
AC∩EO=O,AC、EO面AEC,∴FO⊥面AEC
又EC面AEC,∴FO⊥EC
过点F做FM⊥EC于M,连OM,
又FO⊥EC, FM∩FO=F, FM、FO面FMO,∴EC⊥面FMO
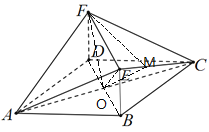
OM面FMO,∴EC⊥MO
∴∠FMO即为二面角A-EC-F的平面角
AC⊥面BEFD, EO面BEFD,∴AC⊥EO
又O为AC的中点,∴EC=AE=![]()
Rt△OEC中,OC=![]() , EC=
, EC=![]() ,∴OE=
,∴OE=![]() ,∴OM =
,∴OM =![]()
Rt△OFM中,OF=![]() , OM =
, OM =![]() ,∴FM =
,∴FM =![]()
∴cos∠FMO=![]()
即二面角A-EC-F的余弦值为![]()
解法三:
连接AC交BD于O,连接EO、FO
菱形ABCD中,∠BAD=60°,∴BD=AB=2
矩形BEFD中,FO=EO=![]() ,EF=2,EO+FO=EF,∴FO⊥EO
,EF=2,EO+FO=EF,∴FO⊥EO
又AC⊥面BEFD, FO面BEFD,∴FO⊥AC,
AC∩EO=O,AC、EO面AEC,∴FO⊥面AEC
又∵EB⊥面ABCD,
∴∠EAB即为EA与平面ABCD所成的角
在Rt△EAB中,cos∠EAB=![]() 又AB=2,∴AE=
又AB=2,∴AE=![]()
∴EB=DF=1
在Rt△EBC、Rt△FDC中可得FC=EC=![]()
在△EFC中,FC=EC=![]() ,EF=2,∴
,EF=2,∴![]()
在△AEC中, AE=EC=![]() ,O为AC中点,∴OE⊥OC
,O为AC中点,∴OE⊥OC
在Rt△OEC,OE=![]() , OC=
, OC=![]() ,∴
,∴![]()
设△EFC、△OEC在EC边上的高分别为h、m,
二面角A-EC-F的平面角设为θ,
则cosθ=![]()
即二面角A-EC-F的余弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某实验单次成功的概率为0.8,记事件A为“在实验条件相同的情况下,重复3次实验,各次实验互不影响,则3次实验中至少成功2次”,现采用随机模拟的方法估计事件4的概率:先由计算机给出0~9十个整数值的随机数,指定0,1表示单次实验失败,2,3,4,5,6,7,8,9表示单次实验成功,以3个随机数为组,代表3次实验的结果经随机模拟产生了20组随机数,如下表:
752 | 029 | 714 | 985 | 034 |
437 | 863 | 694 | 141 | 469 |
037 | 623 | 804 | 601 | 366 |
959 | 742 | 761 | 428 | 261 |
根据以上方法及数据,估计事件A的概率为( )
A.0.384B.0.65C.0.9D.0.904
