Question

【题目】已知抛物线：上的点到其焦点的距离为.

（Ⅰ）求的方程；

（Ⅱ） 已知直线不过点且与相交于，两点，且直线与直线的斜率之积为1，证明：过定点.

Answer 1

【答案】(Ⅰ)y2=x；(Ⅱ)证明见解析.

【解析】试题分析：由题意求得，再根据抛物线的定义推导出，求得的值，代入即可求得的方程证法一：设直线的方程为，联立方程解出，代入求出结果；证法二：设

表示出，设：，联立直线与抛物线方程得，，代入求出结果；证法三：设：，联立直线与抛物线方程，代入，化简求出结果

解析：（Ⅰ）由题意，得，即.

由抛物线的定义，得.

由题意，.解得，或（舍去）.

所以的方程为.

（Ⅱ）证法一：设直线的斜率为（显然），则直线的方程为，则.

由消去并整理得 .

设，由韦达定理，得，即.

.所以.

由题意，直线的斜率为.

同理可得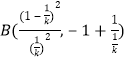，即.

若直线的斜率不存在，则.解得，或.

当时，直线与直线的斜率均为，，两点重合，与题意不符；

当时，直线与直线的斜率均为，，两点重合，与题意不符.

所以，直线的斜率必存在.

直线的方程为 ，即.

所以直线过定点.

证法二：由（1），得.

若的斜率不存在，则与轴垂直.

设，则，.

则 .

（，否则，，则，或，直线过点，与题设条件矛盾）

由题意，，所以.这时，两点重合，与题意不符.

所以的斜率必存在.

设的斜率为，显然，设：，

由直线不过点，所以.

由消去并整理得.

由判别式，得.

设，，则①，②，

则 .

由题意，.

故 ③

将①②代入③式并化简整理得，即.

即，即.

又，即，所以，即.

所以：.显然过定点.

证法三：由（1），得.

设：，由直线不过点，所以.

由消去并整理得.

由题意，判别式.

设，，则①，②

则 .

由题意，，即③

将①②代入③式得，即.

所以：.显然过定点.