题目内容
数列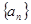 的各项均为正数,
的各项均为正数,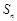 为其前
为其前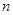 项和,对于任意
项和,对于任意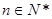 ,总有
,总有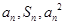 成等差数列.
成等差数列.
(1)求数列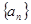 的通项公式;
的通项公式;
(2)设数列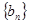 的前
的前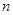 项和为
项和为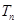 ,且
,且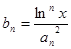 ,求证:对任意实数
,求证:对任意实数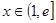 (
(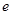 是常数,
是常数,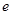 =2.71828
=2.71828 )和任意正整数
)和任意正整数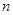 ,总有
,总有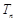
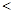 2;
2;
(3)正数数列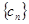 中,
中,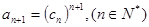 .求数列
.求数列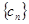 中的最大项。
中的最大项。
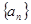 的各项均为正数,
的各项均为正数,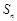 为其前
为其前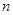 项和,对于任意
项和,对于任意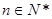 ,总有
,总有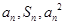 成等差数列.
成等差数列.(1)求数列
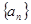 的通项公式;
的通项公式;(2)设数列
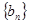 的前
的前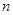 项和为
项和为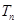 ,且
,且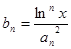 ,求证:对任意实数
,求证:对任意实数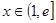 (
(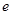 是常数,
是常数,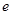 =2.71828
=2.71828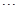 )和任意正整数
)和任意正整数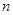 ,总有
,总有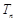
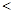 2;
2;(3)正数数列
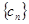 中,
中,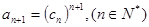 .求数列
.求数列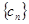 中的最大项。
中的最大项。(1)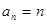 .(
.(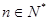 ) (2)见解析 (3)
) (2)见解析 (3)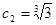
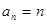 .(
.(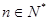 ) (2)见解析 (3)
) (2)见解析 (3)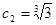
【错解分析】(1)对
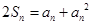 的转化,要借助于
的转化,要借助于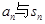 的关系。
的关系。(2)放缩法是此题的难点。
【正解】解:(1)由已知:对于
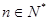 ,总有
,总有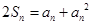 ①成立
①成立∴
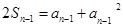 (n≥2)②
(n≥2)② ①--②得
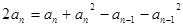
∴
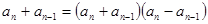
∵
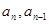 均为正数,∴
均为正数,∴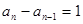 (n≥2)
(n≥2)∴数列
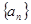 是公差为1的等差数列
是公差为1的等差数列又n=1时,
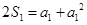 ,解得
,解得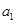 =1∴
=1∴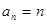 .(
.(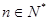 )
)(2)证明:∵对任意实数
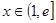 和任意正整数n,总有
和任意正整数n,总有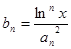 ≤
≤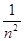 .
.∴
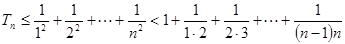
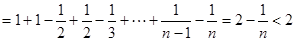
(3)解:由已知
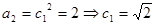 ,
, 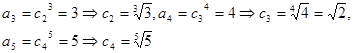
易得
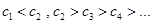
猜想n≥2时,
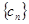 是递减数列.令
是递减数列.令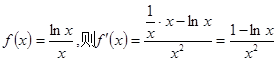
∵当
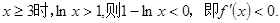
 ∴在
∴在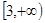 内
内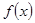 为单调递减函数.
为单调递减函数.由
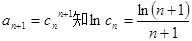 .
.∴n≥2时,
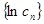 是递减数列.即
是递减数列.即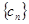 是递减数列.
是递减数列.又
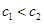 ,∴数列
,∴数列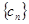 中的最大项为
中的最大项为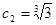 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
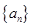 中,若
中,若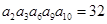 ,则
,则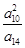 的值为
的值为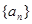 满足:
满足: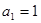 ,
,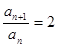 ,数列
,数列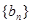 满足:
满足: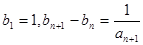 ,(以上
,(以上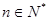 ),则
),则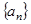 前
前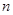 项和为
项和为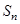 ,首项为
,首项为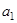 ,且
,且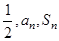 等差数列.
等差数列.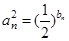 ,设
,设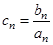 ,求数列
,求数列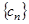 的前
的前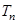 .
.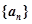 中,
中,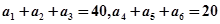 ,则前9项之和等于( )
,则前9项之和等于( )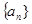 的前n项和
的前n项和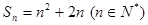 .
.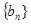 是等比数列,公比为
是等比数列,公比为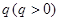 ,且满足
,且满足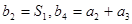 ,求数列
,求数列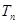 .
.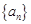 为公比
为公比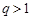 的等比数列,若
的等比数列,若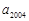 和
和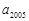 是方程
是方程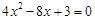 的两根,则
的两根,则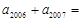 ______.
______.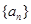 的前
的前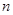 项和为
项和为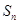 ,若
,若 ,则
,则 .
. 的前n项和为
的前n项和为
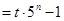 ,则
,则