题目内容
世博会期间,某班有四名学生参加了志愿工作.将这四名学生分配到 、
、 、
、
三个不同的展馆服务,每个展馆至少分配一人.若甲要求不到 馆,则不同的分配方案有
馆,则不同的分配方案有
( )
 、
、 、
、
三个不同的展馆服务,每个展馆至少分配一人.若甲要求不到
 馆,则不同的分配方案有
馆,则不同的分配方案有 ( )
A.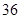 种 种 | B. 种 种 | C.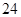 种 种 | D. 种 种 |
C
分析:根据题意中甲要求不到A馆,分析可得对甲有2种不同的分配方法,进而对剩余的三人分情况讨论,,①其中有一个人与甲在同一个场馆,②没有人与甲在同一个场馆,易得其情况数目,最后由分步计数原理计算可得答案.
解答:解:根据题意,首先分配甲,有2种方法,
再分配其余的三人:分两种情况,①其中有一个人与甲在同一个场馆,有A33=6种情况,
②没有人与甲在同一个场馆,则有C32?A22=6种情况;
则若甲要求不到A馆,则不同的分配方案有2×(6+6)=24种;
故选C.
解答:解:根据题意,首先分配甲,有2种方法,
再分配其余的三人:分两种情况,①其中有一个人与甲在同一个场馆,有A33=6种情况,
②没有人与甲在同一个场馆,则有C32?A22=6种情况;
则若甲要求不到A馆,则不同的分配方案有2×(6+6)=24种;
故选C.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 20
20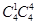 种
种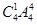 种
种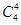 种
种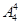 种
种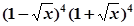 的展开式中
的展开式中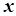 的系数是( )
的系数是( )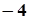
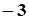
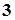
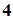
 ,
,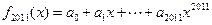 ,求
,求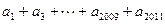 的值;
的值; ,求
,求 中含
中含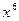 项的系数;
项的系数;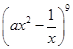 的展开式中常数项为84,其展开式中各项系数之和为__________.
的展开式中常数项为84,其展开式中各项系数之和为__________.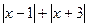 >
>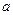 ,对一切实数
,对一切实数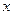 都成立,则实 数
都成立,则实 数