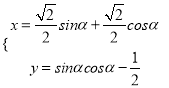题目内容
【题目】若函数![]() ,
,![]() ,对任意的
,对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 具有性质
具有性质![]() .
.
(1)判断函数![]() 和
和![]() 是否具有性质
是否具有性质![]() ,说明理由;
,说明理由;
(2)若函数![]() ,
,![]() 具有性质
具有性质![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() (
(![]() )在实数集
)在实数集![]() 上具有性质
上具有性质![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 具有性质
具有性质![]() ,
,![]() 不具有性质
不具有性质![]() ,理由见详解;(2)
,理由见详解;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)对函数![]() 根据性质
根据性质![]() 的定义容易证明;对函数
的定义容易证明;对函数![]() 只需举反例即可说明;
只需举反例即可说明;
(2)根据函数的单调性,结合性质![]() 的定义,解方程即可求得;
的定义,解方程即可求得;
(3)一方面要保证函数的定义域为![]() ,另一方面要保证性质
,另一方面要保证性质![]() ,据此列不等式组求解即可.
,据此列不等式组求解即可.
(1)函数![]() 的定义域为
的定义域为![]() ,又
,又![]()
若![]() ,则
,则![]() ,
,
对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]()
故函数![]() 具有性质
具有性质![]() .
.
函数![]() 的定义域为
的定义域为![]() ,
,
令![]() ,则
,则![]() ,不存在
,不存在![]() ,
,
使得![]() ,
,
故![]() 不具有性质
不具有性质![]() .
.
(2)因为![]() ,
,![]() 是单调增函数,
是单调增函数,
若其具有性质![]() ,只需
,只需![]()
解得![]() ,故
,故![]() .
.
(3)![]() 等价于
等价于![]()
故![]()
因为![]() ,要使得函数
,要使得函数![]() (
(![]() )在实数集
)在实数集![]() 上具有性质
上具有性质![]()
则一方面要保证函数![]() 定义域为
定义域为![]() ,
,
则只需要分母不为零,在![]() 上恒成立,故
上恒成立,故![]() ,解得
,解得![]() ;
;
另一方面要保证关于![]() 的方程
的方程![]() 有两个不同实数根,
有两个不同实数根,
故![]() ,解得
,解得![]() .
.
综上所述:![]() .
.

练习册系列答案
相关题目
【题目】为普及学生安全逃生知识与安全防护能力,某学校高一年级举办了安全知识与安全逃生能力竞赛,该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛,现将所有参赛选手参加笔试的成绩(得分均为整数,满分为![]() 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)求表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)按规定,预赛成绩不低于![]() 分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为
分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.